Activation Function [활성함수]

활성함수란 ? 간단하게 인공신경망 딥러닝에서 입력을 변환하는 함수를 활성함수라고하며 크게 Relu , Sigmoid , Tahn함수가 존재한다.

 

즉 활성 함수의 선택에 따라 결과 값이 달라진다, 이 말은 다시말하면 적절한 활성함수를 사용하는 것은 매우 중요하다 할수 있다.

활성함수의 개념을 표현한 그림이다 . 

 input data -> activation function -> output data 로 이해하면 될것이다.

 

1. unit step function 

signal & system 에서 아주 자주보던 함수다 

델타함수를 적분하면 튀어나오던 함수다.

활성함수로 사용한다면  f(y) y= wx+b . f() is activation 에서 y값이 0보다 큰구간의 값만 필터로 가지겠다는 의미로 생각한다.

---

2. Sigmoid  - Logistic function / linear multi perceptron에서 비선형값을 얻기 위하여 사용하기 시작함 . 

 

탄젠트함수를 옆으로 기울인 모양의 함수 그래프가 나온다 

만약 시그모이드 함수 s(t)의 t를 +limite & -limite로 보낸다고 하면 아래의 그래프와 유사한 값으로 수렴하게 되겠다.

 

특징

1. 함수값은 0~1 사이의 값

2. 중간 값은 1/2

3. 매우 큰 값을 가지면 함수값은 거의 1, 작은값은 0을가짐.

 

단점

1. Gradient Vanishing 발생 .

미분함수에 대해 x=0에서 max 1/4를 가지며 , input 값이 일정이상 올라가면 미분값이 거의 0에수렴하게됨 , |x|값이 커질수록 

Gradient Backpropagation시 미분값이 소실될 가능성이 있음.

 

2. 함수값의 중심은 0이아니다.

학습이 느려질 가능성이 있음, zigzag 형태로 만들어 학습을 느리게만드는 원인이됨.

 

3. exp함수 사용시 비용이크다. 

1. sigmoid Fucntion & derivative sigmodi function

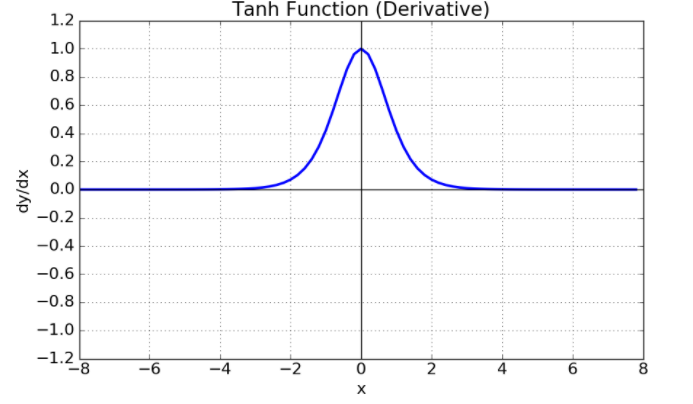
3. Tahn() - 쌍곡선 함수 

 

1. 시그모이드 함수를 변형하여 얻을수있음 .

2. 함수의 중심값이 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결함.

3. 미분시, 일정값 이상 커지면 gradient Vanishing문제가 존재함 . 

4. relu

 

특징.

1. x>0 이면 기울기 1을가지는 직선 , x<0이면 함숫값이 0이다.

2. sigmoid , tanhg함수와 비교시 학습이 훨씬 빠르게 진행됨,

3. 비용이 크지않고 구현이 간단.

4. x<0인 값들에 대해 기울기가 0이기때문에 뉴런이 죽을 수 있는 단점이 존재함.

 

5. Leakly Relu

- Relu 의 Dying Relu (Relu)의 뉴런이 죽는 현상을 해결하기 위해 나온 함수, 

0.01대신 다른값이용가능.

1. 음수의 x값에 대해 미분값이 0이 되지않음 . 그외는 Relu와 동일한 특징이다.

 

6. PRelu

7 Exponential Linear Unit (ELU)

1. Relu의 모든 장점을 포함한다.

2. Dying Relu문제를 해결함

3. 출력값이 거의 zero-centered에 가까움

4. exp함수 계산비용이 발생함.

 

8. Maxout 

Softmax 

세개 이상으로 분류하는 다중 클래스 분류에서 사용하는 활성함수.

분류될 클래스가 n개라고 한다면 , n차원 벡터를 입력받아 클래스에 속할 확률을 추정하는 함수.