시작하기에 앞서
딥러닝 데이터과학을 시작하기에 앞서 DNN CNN RNN LSTM알고리즘에 대하여 간략하고 상세하게 정리하여 필요할때마다 나만의 블로그로 개념을 체크 및 확인하기위하 딥러닝 알고리즘을 정리하고자 한다.
AI(Aritficial Interlligence)는 인간의 지능을 기계어로 구현한 것이다. 여기서 AI 알고리즘중 Deeplearning/ Machine Learning은 AI를 구현하는 접근 방법중 한분야이다.
DNN의 가장 기초인 퍼셉트론은 단층 퍼셉트론과 다층 퍼셉트론으로 나누어진다.
단층퍼셉트론은 값을 보내는 단계(층)[입력층] 와 값을 받아서 출력하는 단계(층)[출력층]로 나뉘어 지는 반면
중간에 층을 더 추가하여 은닉층을 추가한 모델을 다층 퍼셉트론이라고 한다.
1. 1957.Frank Rosenblatt Perceptron이론 (Single-Layer perceptron)
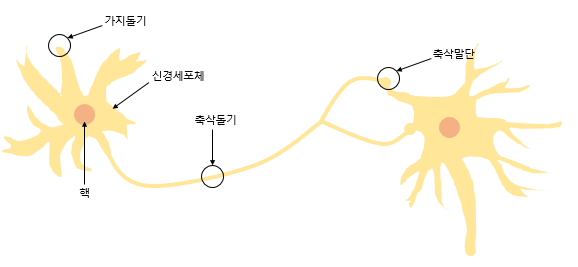
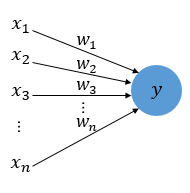
퍼셉트론이란 1957년 로젠플라트가 제안한 초기 형태의 인공신경망이다.
Y= wx.......(1)
Y는 출력값, x는 입력값 w는 가중치값을 나타내고 x, w는 행렬 이다.
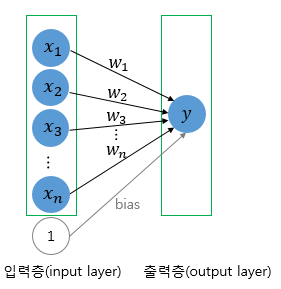
(1).의 수식과 구조는 선형성을 가지는 식으로 다수의 입력으로부터 하나의 결과를 도출하는 알고리즘을 보여주고 있다.
또한 그림 위의 두 그림을 비교해 보자면 안의 원은 인공뉴런을 나타내며 실제 신경세포 뉴런의 신호를 전달하는 축삭돌기의 역할을 퍼셈트론에서 가중치가 대신하며 , 각 인공 뉴런에서 보내진 입력값 x는 각각의 가중치 w와 함께 종착지인 인공뉴런으로 데이터를 전달하는 구조를 가지고 있다.
위의 퍼셉트론을 다시한번 살펴보면 각 입력값당 각각의 가중치가 존재하며 가중치의 값이 크다면 입력값의 중요도가 높아진다는 것을 의미하게 된다.
입력값이 가중치와 곱하여 인공뉴런에 보내지고 , 입력값과 가중치의 곱의 전체의 합이 threshold를 넘으면 출력신호로 1을 출력하고 threshold를 넘지 않으면 0을 출력하는 양상을 보여주게된다. ( Activation Function )
위의 함수는 step function형태로 보여주며 아래의 그래프와 같이 표현할 수 있다.
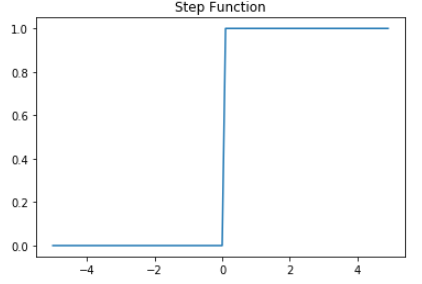
이때 위의 Step function에 사용한 threshold value Θ를 수식으로 표현하면 아래와 같이 표현할 수 있게 된다.
∑wx >= Θ -> y = 1 .......(2)
∑wx < Θ -> y = 0 .......(2.1)
위의 2. 2.1.식에서 threshold value를 좌변으로 넘겨 b (bIas)편향으로 표현할 수 있다.
다시 식 1로 돌아와서 bias값을 퍼셉트론의 입력으로 사용하게 된다면 아래의 그림과 수식으로 표현할 수 있게 된다.
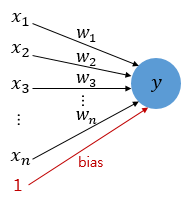
∑wx +b >= 0 -> y = 1 ............(3)
∑wx +b < 0 -> y = 0 .......(3.1)
y=wx+b........(4)
여기서 bias b는 딥러닝이 최적의 값을 찾아야할 중요한 변수중 하나이며 뉴런의 출력값을 변경시키는 함수를 Activation Function이라고 정의한다.
만약 위의 Step Function을 sigmoid Function으로 변경하게되면 퍼셉트론은 곧 이진분류를 수행하는 로지스틱 회귀함수와 동일한 모양을 가지는 것을 확인해 볼수 있게 된다.
Activation Function에 대한 자세한 사항은 아래의 글에 적어 놓았다.
https://hofe-rnd.tistory.com/entry/Activation-Function
Activation Function [활성함수]
활성함수란 ? 간단하게 인공신경망 딥러닝에서 입력을 변환하는 함수를 활성함수라고하며 크게 Relu , Sigmoid , Tahn함수가 존재한다. 즉 활성 함수의 선택에 따라 결과 값이 달라진다, 이 말은 다시
hofe-rnd.tistory.com
요약1. 퍼셉트론 모델과 로지스틱 회귀모델은 활성함수가 step function이냐 sigmoid function이냐의 차이가 존재한다.
Single layer Perceptron의 한계
- 직선 하나로 두영역을 나눌 수 있는 문제에 대하여 구현이 가능하기 떄문에 XOR-GATE는 구현할 수 없다.!!!!!
그렇기 때문에 Single Layer Perceptron에서 Multi Layer Perceptron이 개발되어졌고 Multi Layer Perceptron을 사용하여 여러개의 선을 사용하여 분류를 진행하기 때문에 Single Layer Perceptron에서의 XOR gate문제를 해결하는 방안이 되었다 .
1. Single-Layer Perceptron -Code Python
def and_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = -0.7
result = x1*w1+x2*w2+b
if result <=0:
return 0
else:
return 1
def nand_gate(x1, x2):
w1 = -0.5
w2 = -0.5
b = 0.7
result = x1*w1+x2*w2+b
if result <= 0:
return 0
else:
return 1
def or_gate(x1,x2):
w1 = 0.6
w2 = 0.6
b = -0.5
result = x1*w1+x2*w2+b
if result <= 0:
return 0
else:
return 1
def all_gate(x1,x2):
print(and_gate(x1,x2))
print(nand_gate(x1,x2))
print(or_gate(x1,x2))
return 0
print(all_gate(0,0))
print(all_gate(0,1))
print(all_gate(1,0))
print(all_gate(1,1))C - Single Perceptron ( Rand function input )
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_SIZE 2
#define X_AXIS MAX_SIZE*10
#define Y_AXIS MAX_SIZE*10
typedef struct _perceptron_t
{
int x[MAX_SIZE];
double wight[MAX_SIZE];
double bias;
}pct_t;
pct_t *init_pct(pct_t *pct);
pct_t *set_param(pct_t *pct, double wight, double bias);
int gate(pct_t *pct, double wight, double bias);
pct_t pct[1];
int main()
{
int ret, ret1, ret2;
init_pct(pct);
while(1)
{
ret = gate(pct, 0.5,-0.7);
ret1 = gate(pct, -0.5,0.7);
ret2 = gate(pct, 0.6,-0.5);
printf("and gate :: %d ::: nand gate %d :: or gate%d\n",ret, ret1,ret2);
sleep(1);
}
return 0;
}
pct_t *init_pct(pct_t *pct)
{
int i =0;
for(i=0; i<MAX_SIZE; i++)
{
pct->wight[i] = 0;
}
pct->bias = 0;
return pct;
}
pct_t *set_param(pct_t *pct, double wight, double bias)
{
int i=0;
int num;
srand((unsigned int)time(NULL));
printf("input data ");
for( i =0; i<MAX_SIZE; i++)
{
pct->wight[i] = wight;
pct->x[i] = (int)rand()%10;
printf("%d",pct->x[i]);
}
printf("\n");
printf("Complete Setting param \n");
pct->bias = bias;
return pct;
}
int gate(pct_t *pct, double wight, double bias)
{
int i=0;
float y=0;
int result = -1;
set_param(pct, wight, bias);
for(i=0; i<MAX_SIZE; i++)
{
y += (float)pct->x[i]*pct->wight[i];
}
y += (float)pct->bias;
if( y <= 0)
return 0;
else
return 1;
}2. Multilayer Perceptron
SingleLayer Perceptron과 Multi Layer Perceptron의 가장 큰차이점을 아래의 AND NAND OR GATE를 조합하여 구성한 그림을 보며 살펴보자면
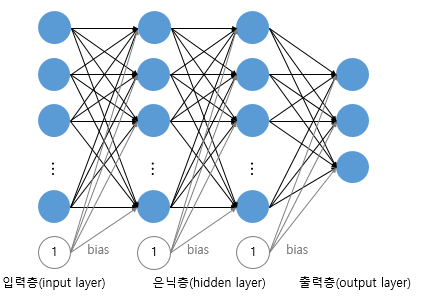
1. SingleLayer Perceptron은 입력층과 출력층으로 구성되어 있지만 Multiple Layer Perceptron (MLP)는 input layer + hidden layer , output layer로 구성되어 있다는 점이 가장큰 차이점이라고 할수 있다. 여기서
Hidden layer가 두개이상인 신경망을 Deep Neural Network라고 정의한다.
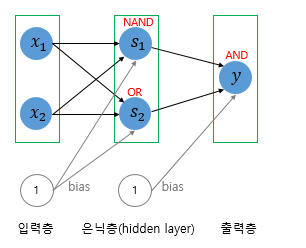
위 Single Layer Perceptron을구성하는 간략한 AND NAND OR gate를 이용하여 XOR gate를 구성하게 된다면 XOR gate는 Hidden layer를 가진 MLP로 코드를 구체화 할 수 있게 된다.
'DataScience > DLML' 카테고리의 다른 글
| Activation Function [활성함수] (0) | 2021.12.01 |
|---|
