Terminology
Timse Series(시계열) ; 동일한 간격의 연속적인 일련의 시간(연속적인)동안 취한 데이터 시퀀스.
Level ; 시계열 데이터의 평균값.
Trend ; 시계열 데이터의 증 감 추세
Seasonality ; 시계열 데이터에서 반복되는 단기적인 주기성 cycle.
| Symbol | discription |
| X | Observation |
| S | Smoothing observation |
| B | Trend factor |
| C | Seasonal index |
| F | The forecast at m periods ahead |
| α | Data smoothing factor α ∈ ( 0, 1 ) |
| β | Trend smooothing factor β ∈ ( 0,1) |
| γ | Seasonal change smoothing factor γ ∈ ( 0,1) |
| Φ | Damped smoothing factor Φ ∈ ( 0,1) |
| t | The index that denotes a time period |
Introduction
Smoothing 기법은 데이터 셋의 noise를 제거하거나 최소화하기 위한 알고리즘 중 하나이다.
즉 일종의 수집해온 real world data set에서 noise를 제거함으로써 데이터의 패턴을 더 두드러지게 보기위해 사용한다.
예를들어 시간기반 음성데이터를 FFT하여 white noise 성분을 제거한 후 고유한 음성데이터를 수집하는 것과 같은 목적이다.
smoothing을 하게 되면 패턴에 기반하여 trend를 예측하기에는 적합하지만 적은량의 sampling 정보를 기반으로 smoothing시 특정한 데이터의 여러 요소가 무시될 수 있는 가능성이 존재한다. ....
4가지 Smoothing 기법
Noisze를 제거한 데이터의 추세나 패턴을 확인하기 위한 목적으로 사용하는 smoothing기법에는
1. Moving average smoothing
2. Exponential smoothing
3. Double exponential smoothing
4. Triple Exponential smoothing
4가지 스무딩 기법이 존재하게 된다.

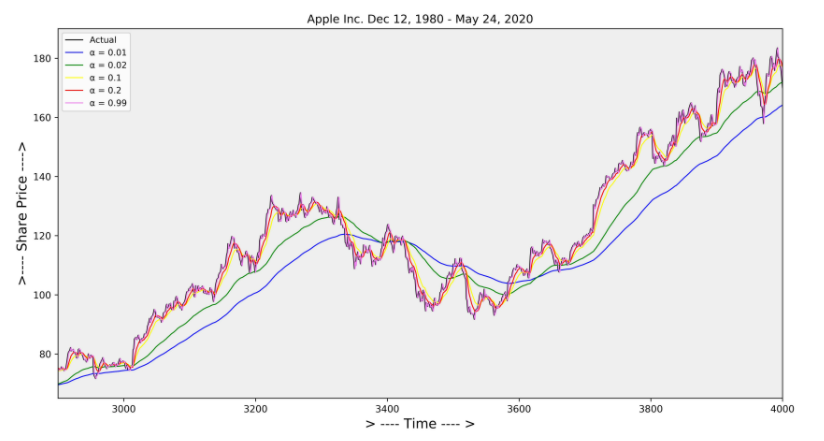

Moving Average Smoothing ( Simple moving Average SMA )
시계열데이터의 분석 및 예측에서 사용되는 가장 간단하고 일반적인 Smoothing 기법이다.
시계열데이터 요소의 마지막 k번째 요소로 구성된 평균으로 도출할 수 있다.


수식을 보면 S는 smoothing observation, X는 observation이다. k는 시계열데이터의 element set의 수로 간주하면되는것 같다.
장기적 추세의 데이터에서는 해당 기법은 smoothing을 잘 수행하지 못한다.
import numpy as np
def moving_avarage_smoothing(X,k):
S = np.zeros(X.shape[0])
for t in range(X.shape[0]):
if t < k:
S[t] = np.mean(X[:t+1])
else:
S[t] = np.sum(X[t-k:t])/k
return S
* 딥러닝이나 데이터 센싱하는 mcu의 관점에서 ? MAS를 사용하고자 한다면 . Window size를 사용하여 큰 데이터를 slide window하여 사용하게 된다.
window size는 원시 관측 데이터의 MAS를 사용하기 위한 관측값의 수를 정의하게 된다.
1. 중앙 이동평균 (Centered Moving Average )
- 시간 t를 기준으로 이전 과 이후의 Raw data를 평균으로 계산하는 방식으로 미래에 대한 데이터 역시 필요하게된다.
- Time series data에서 Trend & Seasonal components를 제거하는 일반적인 방법으로 사용할 수 있으며 예측에서는 자주 사용 하지 않는 방식이다.
. enter_ma(t) = mean(obs(t-1), obs(t), obs(t+1)) // window size가 3인경우의 예시
2. 후행 이동평균 (Tailing Moving Average )
- 시간 t를 기준으로 이전과 그이전의 Raw data를 평균으로 계산하는 방식이다.
. 과거의 관측값을 사용하여 시계열을 예측하게 된다.
. trail_ma(t) = mean(obs(t-2), obs(t-1), obs(t)) // window size가 3인경우의 예시
Exponential Smoothing
Exponential Smoothing 기법은 Weighted moving Average 기법이다 .
Moving Average smoothing은 과거 관측값에 동일하게 Weighted를 부여하게 된다.
factor α 의 값이 0 < α < 1 이기때문에 감소하는 weighted를 부여하여 smoothing을 수행하게 된다.
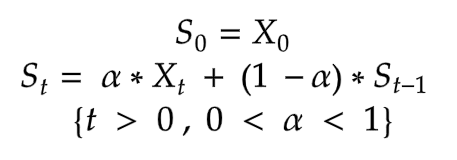

위 수식을 보면 바로 이전에 기대한 수치인 St-1에 (1-α)를 곱하여 재귀적으로 만들었다.
최근 데이터일수록 더 많은 가중치를 주어 시간의 특성을 더 잘 인식 하도록 만든 기법이다.
import numpy as np
def moving_avarage_smoothing(X,k):
S = np.zeros(X.shape[0])
for t in range(X.shape[0]):
if t < k:
S[t] = np.mean(X[:t+1])
else:
S[t] = np.sum(X[t-k:t])/k
return SDouble Exponential Smoothing
단일 Smoothing 은 data에 trend가 존재하면 적합하지 않기때문에 Trend Smoothing factor인 β를 사용하여 개선하게 된다.
t는 Trend가 있지만 Seasonality가 없는 시계열데이터의 modeling에서 적합한 방식으로 사용된다.
α는 level을 smoothing하는 factor로 사용되고
β는 trend를 smoothing하는 factor로 사용하게 된다.
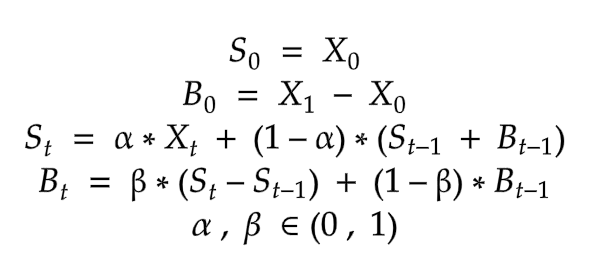

import numpy as np
def double_exponential_smoothing(X,α,β):
S,A,B = (np.zeros( X.shape[0] ) for i in range(3))
S[0] = X[0]
B[0] = X[1] - X[0]
for t in range(1,X.shape[0]):
A[t] = α * X[t] + (1- α) * S[t-1]
B[t] = β * (A[t] - A[t-1]) + (1 - β) * B[t-1]
S[t] = A[t] + B[t]
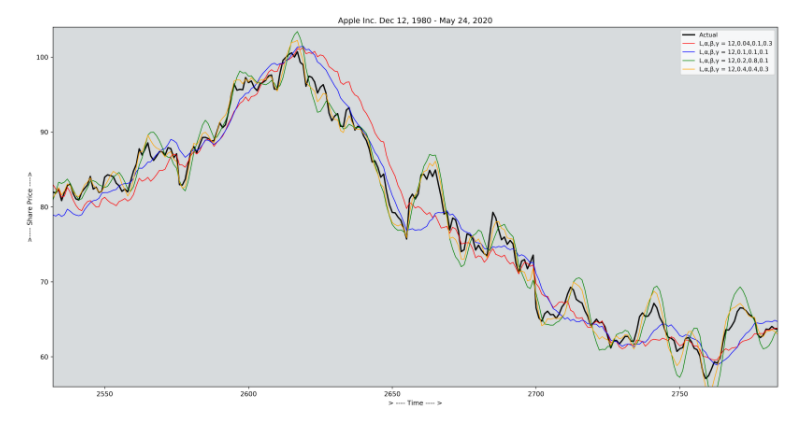
return STriple Exponential Smoothing ( Holt-winters smoothing )
Triple Exponential Smoothing 기법은 Holt-Winters Smoothing이라고도 하며 Seasonal component를 포함한 시계열 데이터를 다룰때 많이 사용하게 되는 기법이다.
아래의 식을 보면 ϕ Factor는 Damping constant로 사용되며 . α, β, γ factor는 MSE가 최소화 되도록 추정되게 된다.
MSE는 2022.01.05 - [DataScience/Data] - [모델 성능지표& Python 코드] Regression - 성능 측정 지표 총정리
에 잘 설명 되어있다.


import numpy as np
def triple_exponential_smoothing(X,L,α,β,γ,ϕ):
def sig_ϕ(ϕ,m):
return np.sum(np.array([np.power(ϕ,i) for i in range(m+1)]))
C, S, B, F = (np.zeros( X.shape[0] ) for i in range(4))
S[0], F[0] = X[0], X[0]
B[0] = np.mean( X[L:2*L] - X[:L] ) / L
m = 12
sig_ϕ = sig_ϕ(ϕ,m)
for t in range(1, X.shape[0]):
S[t] = α * (X[t] - C[t % L]) + (1 - α) * (S[t-1] + ϕ * B[t-1])
B[t] = β * (S[t] - S[t-1]) + (1-β) * ϕ * B[t-1]
C[t % L] = γ * (X[t] - S[t]) + (1 - γ) * C[t % L]
F[t] = S[t] + sig_ϕ * B[t] + C[t % L]
return S
reference
https://machinelearningmastery.com/moving-average-smoothing-for-time-series-forecasting-python/
'DataScience > Data' 카테고리의 다른 글
| [Data processing]- Bayesian Bootstrap Method (0) | 2022.01.21 |
|---|---|
| [Data processing]Bootstrapping /Compiler/ Statistic/ ML 관점의 정리 (0) | 2022.01.21 |
| [interpolation] - Spline method (0) | 2022.01.08 |
| [모델 성능지표& Python 코드] Regression - 성능 측정 지표 총정리 (1) | 2022.01.05 |
| [TREND] Imputation1. (0) | 2021.12.15 |


