머신러닝은 데이터 가공/변환 , 모델 학습/ 예측 그리고 평가의 프로세스로 구성된다.
즉 머신러닝 및 딥러닝 그리고 데이터 모델에대한 최종적인 평가는 성능지표를 통하여 판단하게 된다.
이 이야기는 센서 혹은 여러 비정형 정형데이터를 피나는 노력으로 수집, 전처리, 모델링까지 진행하였다고 하더라도
모델에 대한 평가 지표를 알지못하거나 지표수치가 낮은 수치를 획득하게 된다면 삽질을 하는 순간이 된다.
따라서 논문에 나오는 주요 지표 및 분야별 모델에 대한 성능 지표에 대해 정리해보고자한다.
1. 지표 분류
지표는 주로 regression, classfication, unsupervised models , other로 나누었고 각 파트별로 지표에대한 수식과 그래프적 이유를 설명하고자 한다.
| regression |
| . MAE . MSE . RMSE . RMSSE . MSLE . RMSLE . MPE . MAPE . SMAPE . MASE . R Square . Adjusted R Square |
2. Error 와 Residual 정의
Error와 Residual을 구분하지 않고 에러라고 사용하는 경우가 많긴하지만 엄밀하게 말해서 Error와 Residual은 다른 개념이다.
Error : Population (모집단) 을 대상으로 Regression Forecast 진행시 Real value와 Prediction Value의 차이.
Residual : Population set에서 추출한 (표본집단)sampling을 대상으로 Regression 하여 Sampling set value 와 Prediction value의 차이
Error와 Residual은 엄연히 다른 개녕이지만 둘다 Real value - Prediction value 로 이 값을 최소화 하도록 모델을 구성하는 점에서 모델의 성능을 나타내는 지표로 볼 수 있으며 Population set과 Sampling set 의 대상에 따라 regression problem을 해결하는가에 따라 구분되어 Model을 구성하는 부분은 동일하다.
머신러닝이나 데이터분석시 Population set 보단 Sampling set을 이용하여 Residual이 정확하지만 Error의 개념으로 아래 내용을 작성하도록 하겠다.
1. Regression Indicators
- MAE( Mean absolute Error ) 평균 절대 오차
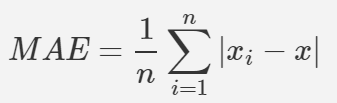
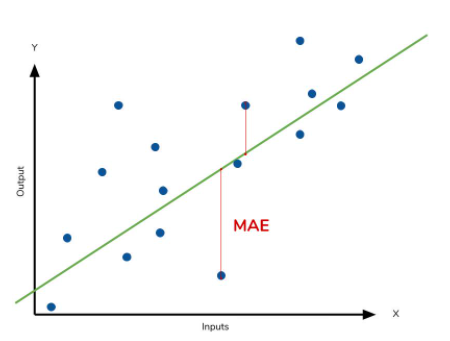
- 실제 값과 예측 값의 차이를 절대값으로 변환하여 평균한 값.
- △X (error) = xi-x
- xi - Prediction value , x ; real value
- MAE =1/n ∑ |△x | , 즉 모든 오차의 절대값을 취한 평균이 된다.
- n ; 오차항의 갯수 △x ; Error
- MAE는 △x의 절대값을 취하여 에러의 크기가 그대로 반영이되는 지표이다. 그렇기때문에 예측 결과물의 에러가 10이 나온것이 5로 나온것 보다 2배가 나쁜 도메인에서 쓰기 적합하다. 이상치(abnormal value)가 많을때 사용하면 용이하다.
- 에러의 크기가 그대로 반영되기때문에 수치가 낮을수록 정확성이 높다는것으로 생각하면된다
- ( 실제값과 예측값의 에러가 낮다 -> 모델이 근사적으로 일치하는 모델이된다 )
- regression에서 회귀 지표로 사용된다.
- code
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_tert,y_pred)
- MSE( Mean Squared Error )
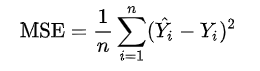
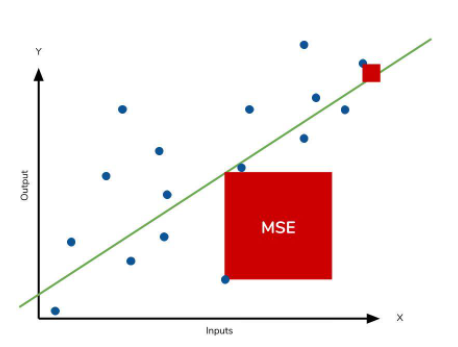
- 실제 값과 예측 값의 차이를 제곱하여 평균한 값.
- MSE = E [ (X - Xi)^2 ]
- X-Xi = Error , X = real value , Xi = Prediction Value ,
- 즉 에러 △X의 넓이의 합의 평균이다.
- 특이값이 존재하면 수치가 많이 늘어난다 ( 제곱하기 때문 )
- 통계적 추정의 정확성에 대한 질적인 척도로 수치가 작을수록 정확성이 높은것으로 판단한다.
- regression 진행시 손실함수로 자주 사용된다. 정확성에 대한개념은 회귀에서 적용되지 않기때문이다.
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)** 즉 예측 값과 실제 값을 MSE방식의 손실함수를 사용하여 점수를 산정한후 옵티마이저를 활용하여 가중치를 업데이트하는 방식이다. Training동안 모니터링을 통하여 MAE를 활용하여 예측값을 측정하게 된다 .
- RMSE ( Root Mean Square Error )
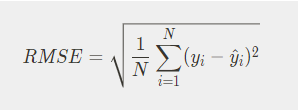
- MSE 값은 Error의 제곱의 평균으로 실제 Error보다 큰 Error들의 평균을 가지는 특성이 있있다 그렇기 때문에 MSE값에 √ root를 씌워 RMSE 값을 사용하게 된다. (정밀도의 개념)
- 평균을 낼떄 MSE는 1/n을 사용하지만 RMS는 1/ √n 을 사용하게된다. 즉 MSE보다 RMSE의 평균값은 커질수 밖에없다.
- MAE와 MSE의 장점을 모두 가지고 있게된다.
- Error에 제곱하여 루트N으로 나누게 되어 가중치는 높아진다. 다시말해 큰 Error값에 대해 패널티를 크게준다.
- 즉 MSE보다 RMSE가 더 RUBUST하다고 말할수 있다.
- Error 손실이 기하급수적으로 올라가는 상황에서 자주 사용하게 된다. [머신러닝에서 자주쓰게된다 abnormal한 즈즉 specific 한 value에 영향을 덜 받기 위해 쓰는것이다 .]
- RMSE값이 적을 수록 더 좋은 성능이라고 평가할 수 있다.
import numpy as np
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y_test, y_pred)
np.sqrt(MSE)
# sklearn 은 mse만 제공하기 때문에 rmse는 직접 만들어 써야한다.
- RMSSE( Root Mean Squared Error )
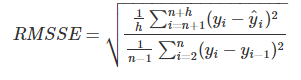
yi; real value
yi hat ; model prediction value
n ; train dataset size
h ; test dataset size
- MAPE와 SMAPE는 MAE를 스케릴링하기 위해 데이터의 Real value와 predict value를 활용하기 때문에 오차의 절대값이 같아도 Over or Under estimate여부에 따른 패널티가 불균등하게 부여하게된다.
- 그렇기 떄문에 RMSSE는 MSE를 스케일링할 떄 훈련 데이터를 활용하므로 이러한 불균등 문제에서 독립적이게 된다.
- 훈련데이터에 대해 Navie forecasting하게된다면 MSE값으로 나눠 주기때문에 예측값의 over under estimation에 따른 오차 값이 영향을 받지 않게 된다.
- navie forecast ; y hat = yi-1 , ; i시점의 예측값을 i-1의 실제값으로 예측하는 방법.
import numpy as np
def RMSSE(y_ture, y_pred, y_test):
n = len(y_test)
numerator = np.mean(np.sum(np.square(y_true - y_pred)))
denominator = 1/(n-1)*np.sum(np.square((y_test[1:] - y_test[:-1])))
msse = numerator/denominator
return msse ** 0.5- MSLE(Mean Squared Log Error ) - log error
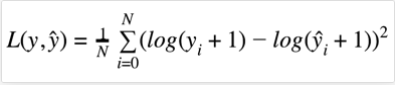
- MSLE의 값은 MSE = E [( Y- Yi)^2]에서 Real value와 prediction value에 Log( ) 를 취하여 Residual 즉 Error Term을 구한 값의 제곱을 취한 값의 평균이다. 즉 MSE에 LOG를 적용한 지표이다.
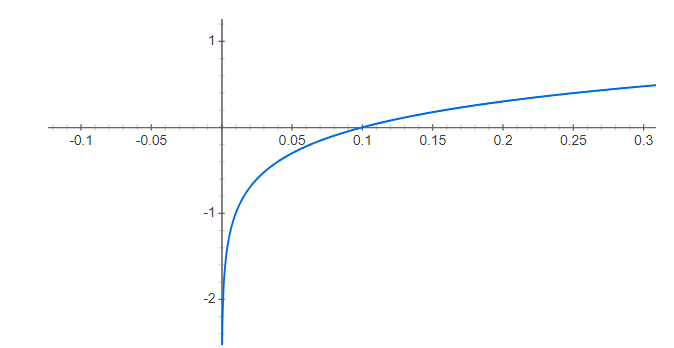
- log의 지수를 보면 y, yi 모두 log(y) - log(yi)가 아닌 log(y+1)- loh(yi+1)이다 즉 그래프 개형상 왼쪽으로 1 shift해준것을 볼 수 있다.
- 이는 y = log(x) 함수의 특성상 x->0으로 무한대로갈때 y값은 음의 무한대의 값을 가지기때문에 왼쪽으로 1 left shift해주었다.
- ** 주의사항 log(x)에서 x>0 커야하는 조건이있다. 즉 MSLE를 사용할떄 real value +1, prediction value+1의 값은 모두 양수여야한다는 조건이다 . (만약 음수의 value라면 문제가 발생한다 .^^ )
- absolute Error 가아닌 상대적 오차를 기준으로 평가하게 된다면 사용하게 된다.
- 만약 Real value 와 Prediction value에 음수가 있다면 오류가 날 경우가 있으니 주의해야 한다 .
from sklearn.metrics import mean_squared_log_error
mean_squared_log_error(y_test, y_pred)- RMSLE(Root Mean Squared Log Error ) - Log Error
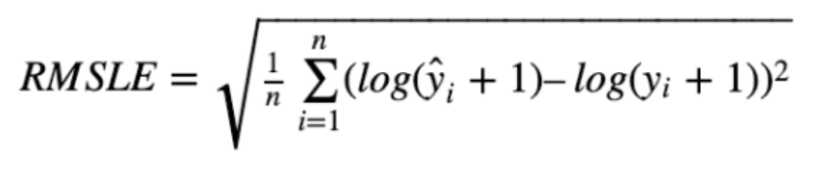
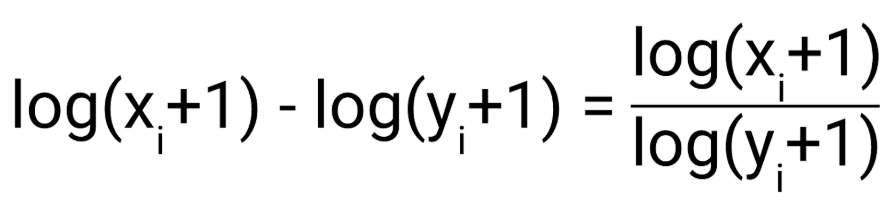
- RMSE =√E[ (x-xi)^2 ) ] 의 real value x와 prediction value xi에 log( ) 를 취한후 residual값의 제곱의 평균에 Root를 취한 값이다.
- RMSLE의 가장큰 특징은 log scale로 1. outlier (극단 값 ) 에 강하다(rubust )한 특징이 있다. (즉 이상치의 값이 전체 데이터에 영향을 덜 주도록 제어하는 방식이다 ) 다시 말하면 값의 변동폭이 크지 않다.
- * outlier은 통계적 자료분석의 결과를 왜곡시키거나, 자료 분석의 적절성을 위협하는 변수값 또는 사례를 말한다.
- 분포의 집중경향치의 값을 왜곡시키거나, 상관계수 추정치의 값을 왜곡시키는 개체 또는 변수의 값을 의미
- 모수추정치의 값을 왜곡시키는 개체 또는 변수의 값으로 일반적인 경향에서 벗어나는 사례를 지칭하게된다.
- 분포의 집중경향치의 값을 왜곡시키거나, 상관계수 추정치의 값을 왜곡시키는 개체 또는 변수의 값을 의미
- 상대적 Error 를 측정하게 해준다. 즉 로그 식이기때문에 error는 상대적 비율을 구하게 된다. 값의 절대적 크기가 커지면 RMSE의 경우 RMSE수치 역시 커지는 경향이 있지만 RUBUST한 성질을 가지고 있기 때문에 RMSLE는 상대적 크기가 동일하다면 RMSLE역시 비슷한 추세를 가진다.
- Under Estimatie에 큰 패널티를 부여하게 한다. RMSLE는 Over Estimation 보다 Under -Estimation에 있어 예측값이 실제값보다 큰경우 보다 예측값이 실제값보다 더클때 더큰 패털티를 부여하게 된다 . log 기반의 지표이기때문에 예측값이 실제값보다 작은 경우 더 큰 패널티를 부여하게 되어있다.
- 만약 Real value 와 Prediction value에 음수가 있다면 오류가 날 경우가 있으니 주의해야 한다 .
import numpy as np
from sklearn.metrics import mean_squared_log_error
MSLE = mean_squared_log_error(y_test, y_pred)
RMSLE = np.sqrt(MSLE)- MAPE( Mean Absolute Percentage Error )
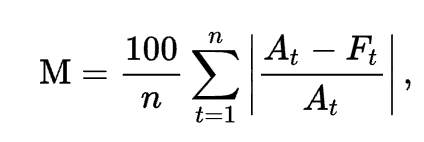
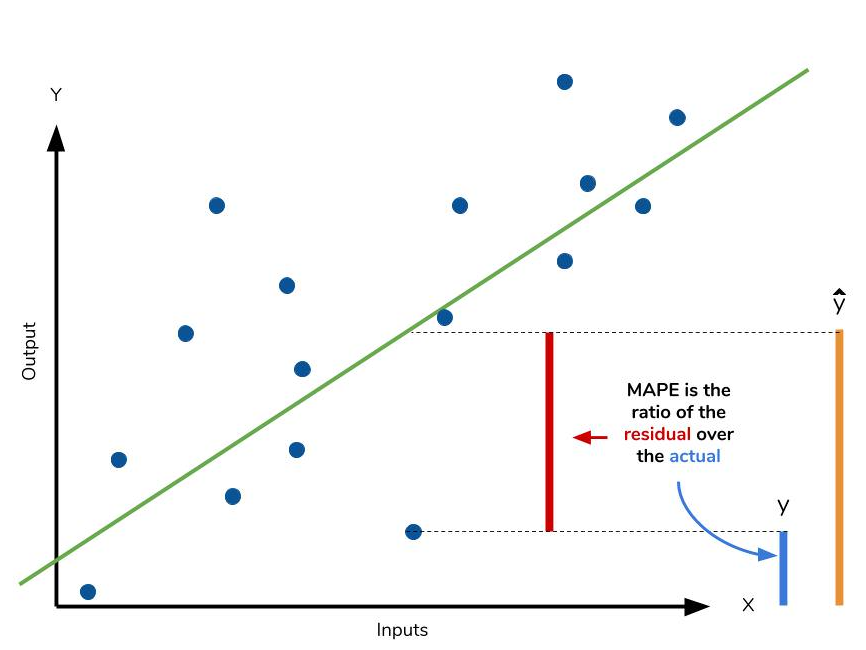
- MAE =1/n ∑ |△x /x | , 즉 모든 오차를 실제값으로 나눈후 절대값을 취한 평균에 *100을하여 퍼센트로 변환한 값.
- At ; real value , Ft; Prediction value 이다 .
- 변동폭을 실제값으로 나누어 보면 비율 상 같은 기준으로 비교할 수 있게 되어 변동성과 관련하여 볼수 있는 지표라고 생각한다.
- 백분율로 된 오차는 Pt= Errot T / Yt 로 주어지게 되고 단위와 관련 없는 값을 도출하게 되어 데이터 SET 에서 예측 성능을 비교할 때 사용하게 된다.
- 만약 Yt 즉 Real value 가 0이라면 결과값은 무한대의 값이 되거나 정의 되지 않은 다는 조건이 있어 .Yt가 0에 가까울수록 극한의 값을 가지게 된다. 그렇기 때문에 측정되는 Real value중 0이 의미가 존재하는 데이터의 경우 문제가 발생하게 된다.
- MAE와 같이 모델에 편향이 존재하기도 한다.
import numpy as np
def MAPE(y_test, y_pred):
return np.mean(np.abs((y_test - y_pred) / y_test)) * 100
MAPE(y_test, y_pred)- MASE ( Mean Absolute Scaled Error )
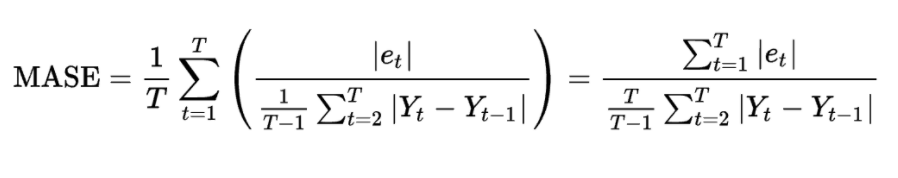
- RMSE, MAPE와 다른 접근방법의 지표로 예측값과 실제값의 차이를 평소에 움직이는 평균 변동폭으로 나눈 값.
- 평소 변동폭에 비해 얼마나 오차가 차이가 나는지를 측정하는 기준.
- MASE 변동성이 큰지표와 변동성이 낮은 지표를 같이 예측할 필요가 있을 때 유용하게 사용됨.
- Loss Function을 사용하여 설정할 수 있음.
import numpy as np
from epftoolbox.evaluation._ancillary_functions import _process_inputs_for_metrics, naive_forecast, _transform_input_prices_for_naive_forecast
from epftoolbox.evaluation import MAE
def MASE(p_real, p_pred, p_real_in, m=None, freq='1H'):
p_real_in = _transform_input_prices_for_naive_forecast(p_real_in, m, freq)
p_pred_naive = naive_forecast(p_real_in, m=m)
p_real_in = p_real_in.loc[p_pred_naive.index]
MAE_naive_train = MAE(p_real_in, p_pred_naive)
p_real, p_pred = _process_inputs_for_metrics(p_real, p_pred)
return np.mean(np.abs(p_real - p_pred) / MAE_naive_train)
"""Function that computes the mean absolute scaled error (MASE) between two forecasts:
.. math::
\\mathrm{MASE}_\\mathrm{m} = \\frac{1}{N}\\sum_{i=1}^N
\\frac{\\bigl|p_\\mathrm{real}[i]−p_\\mathrm{pred}[i]\\bigr|}
{\\mathrm{MAE}(p_\\mathrm{real\\_in}, p_\\mathrm{naive\\_in}, m)}.
The numerator is the :class:`MAE` of a naive forecast ``Ynaive_in`` that is built using the insample
dataset ``p_real_in`` and the :class:`naive_forecast` function with a seasonality index ``m``.
If the datasets provided are numpy.ndarray objects, the function requires a ``freq`` argument specifying
the data frequency. The ``freq`` argument must take one of the following four values ``'1H'`` for 1 hour,
``'30T'`` for 30 minutes, ``'15T'`` for 15 minutes, or ``'5T'`` for 5 minutes, (these are the
four standard values in day-ahead electricity markets).
Also, if the datasets provided are numpy.ndarray objects, ``m`` has to be 24 or 168, i.e. the
:class:`naive_forecast` cannot be the standard in electricity price forecasting because the input
data does not have associated a day of the week.
``p_real``, ``p_pred``, and `p_real_in`` can either be of shape
:math:`(n_\\mathrm{days}, n_\\mathrm{prices/day})`,
:math:`(n_\\mathrm{prices}, 1)`, or :math:`(n_\\mathrm{prices}, )` where
:math:`n_\\mathrm{prices} = n_\\mathrm{days} \\cdot n_\\mathrm{prices/day}`
Parameters
----------
p_real : numpy.ndarray, pandas.DataFrame
Array/dataframe containing the real prices.
p_pred : numpy.ndarray, pandas.DataFrame
Array/dataframe containing the predicted prices.
p_real_in : numpy.ndarray, pandas.DataFrame
Insample dataset that is used to compute build a :class:`naive_forecast` and compute its :class:`MAE`
m : int, optional
Index that specifies the seasonality in the :class:`naive_forecast` used to compute the normalizing
insample MAE. It can be be ``'D'`` for daily seasonality, ``'W'`` for weekly seasonality, or None
for the standard naive forecast in electricity price forecasting,
i.e. daily seasonality for Tuesday to Friday and weekly seasonality
for Saturday to Monday.
freq : str, optional
Frequency of the data if ``p_real``, ``p_pred``, and ``p_real_in`` are numpy.ndarray objects.
It must take one of the following four values ``'1H'`` for 1 hour, ``'30T'`` for 30 minutes,
``'15T'`` for 15 minutes, or ``'5T'`` for 5 minutes, (these are the four standard values in
day-ahead electricity markets).
Returns
-------
float
The mean absolute scaled error (MASE).- SMAPE( Symmetric Mean Absolute Percentage Error )
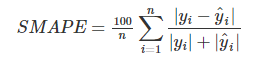
- MAPE의 값은 Y값에 의존적인 경향이 강하다 . 이를 보안하기 위해 고안된 평가모델이다.
import numpy as np
def SMAPE(y_test, y_pred):
return np.mean((np.abs(y_test-y_pred))/(np.abs(y_test)+np.abs(y_pred)))*100- MPE ( Mean Percentage Error )
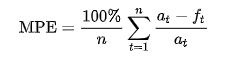
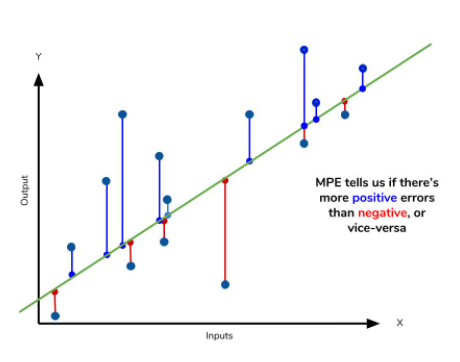
- MAPE에서 절대값을 제외한 지표
- 모델의 성능이 UnderPerformance(+) 인지 OverPerformance(-)인지 판단
- 예측의 편향성을 측하는데 사용할수 있으며 MAPE와같이 Real value At가 0이되면 안된다는 단점이 존재한다.
import numpy as np
def MAE(y_test, y_pred):
return np.mean((y_test, y_pred) / y_test) * 100)
MAE(y_test, y_pred)- R2 (R Square) - 분산기반 예측 성능 평가
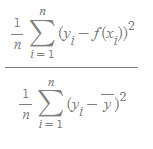
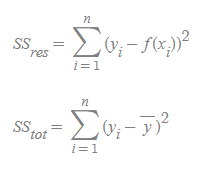
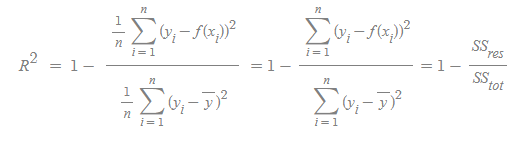
- 위 식을 바라보면 y-bar는 y의 평균을 말하며 위 식의 값이 작아진다는 의미는 실제 데이터의 분산에비해 Regression의 Error이 작다는 이야기다. 0에 가까운 값을 가질 수 있다.
- SSres 는 제곱의 오차항이며 SStot는 전체 제곱의 항이다.
- RMSE는 에러의 크기에 대한 정보는 주지만, 실제 데이터 값의 크기의 정보는 주지 않는다. 즉 RMSE의 값이 같더라도 , 데이터 값의 크기가 서로 다르면 성능은 다르게 평가되어야 하는데 이때 사용하는것이 R2 평가 모델이다.
- 에러의 크기(주로 MSE)를 데이터의 크기(주로 데이터의 분산데이터)로 선택하여 나누어준다.
- 즉 R2의 성능은 1에 가까울 수록 좋은 성능을 나타낸다
- 결정계수 방법은 Regression의 정합성을 판단시 자주 사용하는 방법이고 . 에러의 자체 크기 보단 실제 데이터의 분산과 Regression 에러간의 비율과 관련된 값이다. 즉 변화량대비 Error의 발생 정도에 집중하는 상대값이다.
from sklearn.metrics import r2_score
r2 = r2_score(y, lr.predict(x_2))- adjusted R squared
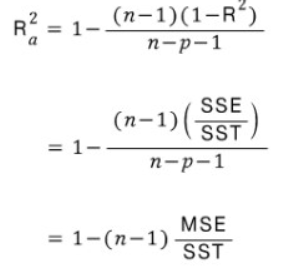
- 다변량 Regression 분석에서 독립변수가 유의하거나 , 유의하지 않거나 독립변수의 수가 많아지면 R squared 지수가 높아진다.
- P는 독립변수의 갯수로 p가증가시 R-square의 값도 증가하는 영향을 상쇄하는 FACTOR로 작용한다.
- R2 보다 Adjusted R2가 값이 더작게 나오는 경향이 있다.
보통 데이터모델링, 머신러닝, 딥러닝등의 모델링시 바로 알고리즘 모델링하여 실험 하는 경우가 많다.
하지만 문제를 해결하기 위해 여러 논문 혹은 방식을 분석을 한 후 모델링을 올바르게 그리고 접근한 방식 중 최선의 방식이 무엇인지 모른다면 모델링을 제대로 한것인지 알 수 없다. 모델링 방법과 더불어 모델의 성능에 대해 잘 구현됐는지 평가하는 방법에 대해서도 세세하게 짚고 넘어가야 한다.
'DataScience > Data' 카테고리의 다른 글
| [Data processing]- Bayesian Bootstrap Method (0) | 2022.01.21 |
|---|---|
| [Data processing]Bootstrapping /Compiler/ Statistic/ ML 관점의 정리 (0) | 2022.01.21 |
| [interpolation] - Spline method (0) | 2022.01.08 |
| [Data PreProcessing]TimeSeries-Smoothing 기법 정리 (1) | 2022.01.06 |
| [TREND] Imputation1. (0) | 2021.12.15 |


