Smoothing Bootstrap을 공부하다 보면 Kernel Density Estimation개념이 나오게 된다 또한 Bootstrap method를 사용하는 몇몇 논문을 확인하면 Long Term Estimate 기법에서 데이터의 Density를 Estimation하는게 더 유익하다고 한다.
여기서 Density Estimation이 무엇인가 ? 또한 그냥 가볍게 아~ 저게 Kernel이구나 하고 사용하였던 Kernel에 대하여 다루어 보고 KDE가 무엇인지 밝혀보고자 한다 .
Motivation
어떤 데이터의 분포를 파악하는 것은 데이터 분석시 아주 중요한 단계라고 할 수 있다. 실제 데이터 분포는 정규 분포와 같은 형태를 따르지 않고 데이터가 어떤 분포를 따르는지 대체로 알 수 없다. 이럴때 분포를 추정하여 확률 밀도를 구하는 방법은 Histogram, kernel density estimation, K-nearest neighbor 등 의 방법이 있다 .
여기서 KDE를 살펴보기 전에 우선 KDE의 목적은 Probability density P(x)를 구하는 것이 목적이다.
즉 일정한 단위에 데이터가 몇 개나 포함되는지의 수치와 같으므로 P(x)는 아래의 식과 비례하는것을 확인할 수 있다.
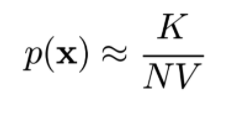
N ; 전체 데이터 Sample number, ( 고정된 값 )
K ; Region안에 있는 데이터의 수
V ; Region의 부피 (크기 고정 )
What's Kernel function ?
Kernel이란 무엇인가 ?
구글에 Kernel을 검색하면 Kernel의 사전적의미는 핵심이라고 한다 여기서 KDE 그리고 Density Estimation에서 의미하는 핵심이라는것이 무언인가 고려해보아야 할것이다.
KED에서 말하는 Kernel은 우선 Kernel function을 알아야 한다 .
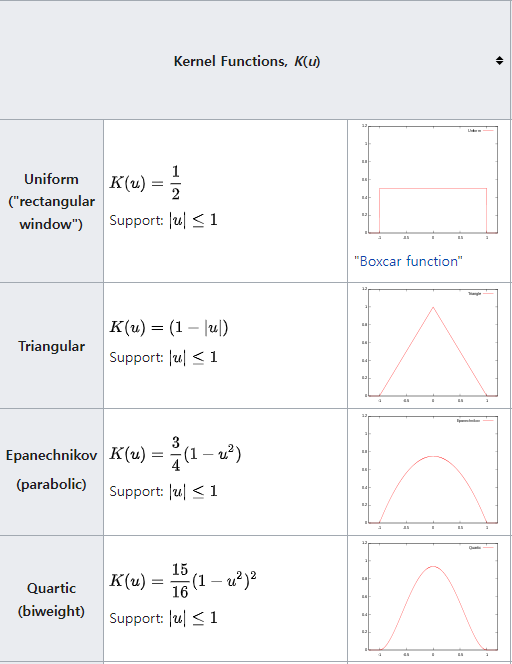
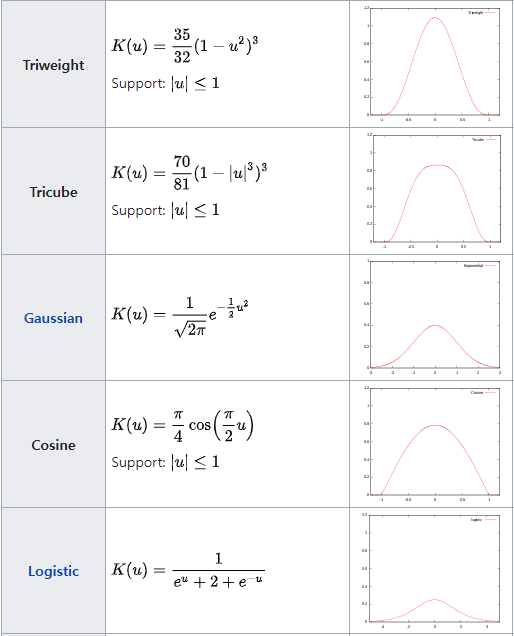
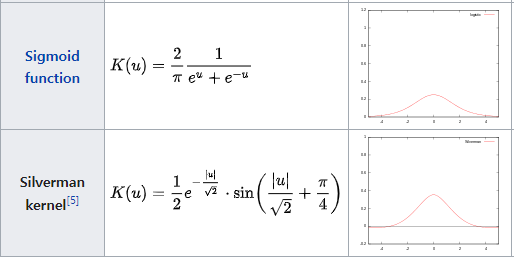
Kernel function은 수학적으로 원점을 중심으로 Symmetric하며 적분값이 1인 Non-Negative fucntion으로 아래의 조건으로 정의된다. - refernece Wikipedia Kernel Statisitics
- Normalization
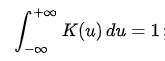
- Symmetry :
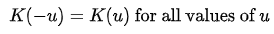
Density Estimate
Density Estimate는 Probabilistic 과 Statistic에서 기본적으로 Unobservable (variable로 보자)한 PDF를 Observation data(General 하게 Population의 Random Sample으로 간주한다) 기반으로 추정하는 것을 원칙으로 한다. 즉 Data와 Variable사이의 관계(본질적 특성)를 파악하는 방식이다.
다시말하자면 Real world에 존재하는 Data Variable중 일부의 Observation data를 활용하여 Origin Variable Model이 가진 특성을 추정하고자 하는 것이 목적이다.
예를들면 전기차량 Autonomous vehicle 혹은 가전에 사용하는 제품의 센서를 통하여 어떤 일련의 데이터를 얻었다고 치면 그 데이터는 하루치 Sensing data이다. 그리고 실제로 매일 Sensing이 된다고 친다면 그 데이터는 제품이 Driving하는 동안 계속해서 측정해낸 Observation data이다. 제품이 Drive되는 조건에 따라 그 일일 데이터량은 매번 다른 데이터를 Sensing할 수 있다. 이러한 단일한 일련의 데이터로는 Sensing Model에 대한 결론을 내리긴 어렵지만 .
이러한 데이터가 주, 달, 계절, 1년, 등 대량으로 쌓이고 데이터의 Period혹은 상관성이 존재하는 데이터와 함께 분석하다 보면 Origin Model에 대하여 파악할 수 있게 된다. 여기에 어떤 Variable의 가능성 및 척도를 추정하는 것이 Density Estimation이 된다.
맨처음 TimeSeries Paper를 보며 내가 Density Estimation을 이해할때 Density는 질량/부피 Mass/Volume로 정의하여 이해하기에 조금 난해하였지만 . 무선통신 신호처리의 통계분야를 공부할때 Density는 확률밀도(Probability Density)를 의미하고 Density를 Probability Density로 이해하니 의미가 정확하게 이해가 되었다.
여기서 Probability Density Function ( PDF )는 확률변수 (Random variable)을 의미하고. Random Variable의 distribution을 나타내는 함수로 $f(x)와 range[a.b]에 대해 Random Variable X가 range에 포함할 확률 $P(a<=x<=b)를 아래의 식과 같이 표현하게 된다.
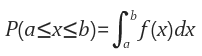
- PDF Condition
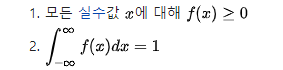
- PDF- CDF의관계
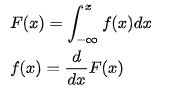
즉 어떤 Observation Data X의 Density를 추정하는것은 X의 PDF를 추정하는것과 같다.
여기서 Observation Data X의 PDF f(x)의 개형이 아래와 같다고 할때
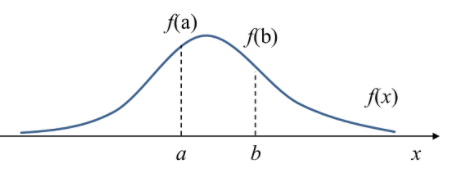
f(a)는 x= a 에서 Probability Density이며 Variable X가 a의 값을 가질 가능성(Relative likelihood)를 나타낸다 라고 할 수 있다.
- Density 와 Probability의 차이
위의 그림과 PDF의 식을 보면 P(x=a) = 0이다 하지만 x= a에서의 Density는 f(a)로 0이아니다.
즉 확률은 x가 a~b구간의 값을 가질 적분값 즉 면적의 값이지만 Density는 PDF의 함수값이고 Density를 구간에대해 적분하면 PDF가 나오게 된다.
Parametric & Non-Parametric
Density Estimation방법 뿐만아니라 Statistic을 정리하다 보면 Parametric과 Non-Parametric을 자주 접하게 된다.
- Parametric statistic은 fixed된 Parameter의 Set이 있는 Probability Distribution으로 모델링 할 수 있는 Population 으로부터 Sample data를 가져오는것으로 가정하는 Statistic의 한 분야이다. [ Mean Variance 가 이에 해당 하는 대표적 예 ]. 데이터가 특정 Distribution을 따른다는 가정하에 파라미터의 종류와 수가 명확하게 정해진 경우를 의미하게 되어 데이터수 에따라 파라미터의 수는 변하지 않게된다 . 모델의 형태를 정한 후 발전시켜나가는 형식으로 알고리즘이 진행되는데 Density estimation에서는 PDF에 대한 모델을 정하여 Data로부터 모델의 파라미터만 추정하는 방식이라고 보면 된다. 이말은 위의 Sensing된 Observation data가 Standard Distribution을 따른다고 할때 observation data 로부터 Mean E[x]와 Var[X]를 구하면 문제가 해결되기 때문에 쉽게 접근할 수 있는 통계라고 볼 수 있다.
- Non-parametric model은 Data를 모델링할때 수학적으로 Distribution의 형태를 (finite-parametric하게 명시적으로) 가정하지 않게된다. [ 간혹 Continuity or Symmetry에 대해서는 가정이 들어가곤 한다 ] Parametric Statistic과 별개로 Non-Parametic은 사전 정보 혹은 사전 지식 없이 ( 데이터가 특정 분포를 따르는 가정이 없기 때문에 ) 순수하게 Observation data ( 튜닝 parameter가 명확하지 않은 ) set으로만 PDF를 추정해야 하는 방식이다. Non-Parametric의 Density estimation의 가장 간단한 형태가 Histogram이고 이 Histogram을 구한후 Normalization을 하여 PDF를 사용하게 된다. 하지만 Histogram은 Bin size 및 시작 점과 boundary에서 Discrete하다는 문제와 High Dimension data는 Memory issue등이 존재하여 사용하기 힘든 문제가 존재한다.
Parametric & Non-Parametric Example
- Parametric model : Linear Regression Logistic regression,Bayesian inference, Neural network(CNN, RNN 등) 등. 모델에 대하여 명확하게 정해진 가정이 존재하기 때문에 분석 및 이해도에 있어 더 접근성이 높지만 가정으로 인하여 유연성이 낮다고 본다.
- Non-Parametric model : Decision Tree, Random Forest, K-nearest neighbor classifier 등. 데이터 모델이 명확하지 않다. 고로 가정을 하지 않게 된다. 상대적으로 Parametric model보다 느릴수 밖에 없지만 더 유연성이 높다.
Kernel Density Estimation
앞서 Kernel function, Density Estimation, 그리고 Parametric / Non-parametric Statstic에 대하여 소개하였다. KDE(Kernel Density Estimation)은 Non-Parametric Density Estimation중의 한 방식으로 Kernel function을 이용하여 Histogram의 문제점을 개선하게된다.
X를 Random Variable, i,i,d한 X1,X2, ... Xn을 Observation Sample Data Set X, K는 kernel function이라고 하였을때 KDE의 Random variable X에대한 PDF는 아래와 같다.
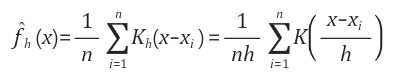
위의 수식에서 h는 Kernel function의 Bandwidth parameter로 h의 크기에 따라 Kernel의 형태가 조절되는 Parameter로, scaled kernel이라고 하고 Kh(x)의 정의는 아래와 같다. 하지만 h의 크기는 Bias of Estimation 과 데이터의 Variance 사이에서 고려해야 한다.
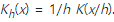
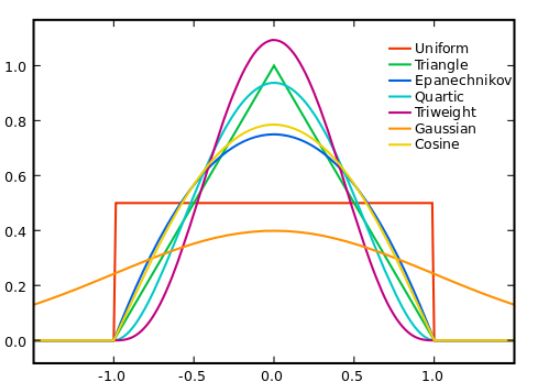
일반적으로 Kernel function에서 Epanechnikov kernel function은 MSE에서 Loss of Efficienct가 가장작아 Optimization하지만 수식의 간편성을 위해 K(x) = Φ(x)로 ,Φ는 Standard Normal Density Function으로 자주 사용한다고 한다 .
K(x-xi)는 Observation data의 각 해당 데이터 값을 중심으로 하는 Kernel function을 생성하게 되고 . Kernel function을 모두 더한후 전체 데이터 개수로 나누게 된다.( Normalization ) .
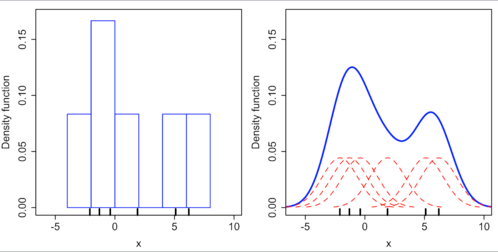
KDE를 적용하여 PDF를 구하게 된다면 Discrete한 데이터의 Graph개형인 Histogram함수의 Bandwidth와 Bin size를 조정하여 Kernel function을 적용하여 Smooth한 것으로 바라볼 수 있게 된다.
h; Bandwidth Selection
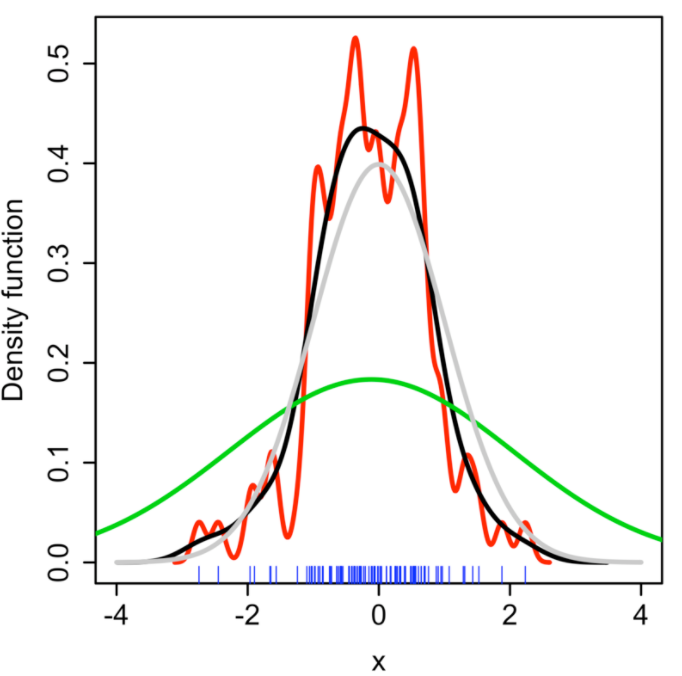
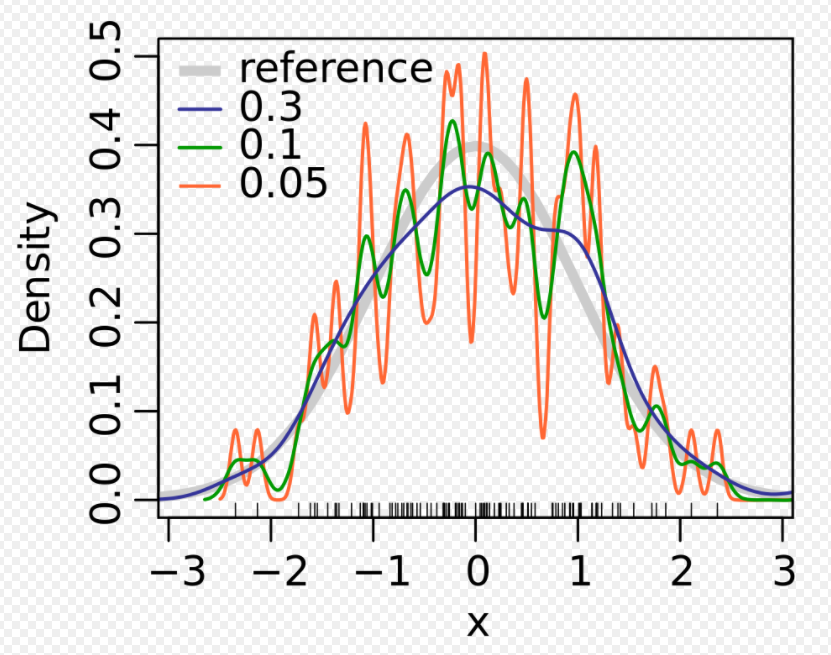
Kernel의 Bandwidth는 결과 추정치에 큰 영향을 주는 Free Parameter이다.
위의 그래프에서 회색 곡선은 실제 Density이다( Mean은 0이고 Variance가 1인 Standard Density Distribution ).
빨간 곡선은 Bandwidth parameter h = 0.05 일때 Spurious data artifacts포함된 Undersmoothed 된 그래프이다.
초록색 곡선은 Bandwidth parameter h = 2일때 Histogram의 기본적인 data의 추세를 모두 가리게 된 OverSmooth 그래프이다.
검정색 곡선은 Bandwidth Parameter h = 0.337일때 Density Estimation 이 True Density Graph인 회색 곡선과 유사하기 때문에 Optimal Smooth로 간주하게 된다.
여기서 Bandwidth Parameter h 가 limit -> 0인 상황은 Smoothing이 없는 상황이 되고 여기의 Estimation value는 Sample좌표를 중심으로 n Delta function의 합이 된다.
반대로 Bandwidth Parameter h가 limit -> infinte일 때 Smoothing으로 Sample의 Mean을 중심으로 사용된 Kernel의 Shape를 유지하게 된다.
그러면 여기서 검정색 곡선의 Bandwidth를 추정하기 위한다면 어떻게 해야하는가?
일반적으로 Optimally parameter를 얻기 위해서 Loss function과 MISE를 사용하게 된다.
MISE (Mean Integrated Squared Error )
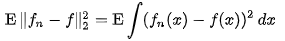
통계학에서 MISE는 Density Estimation에서 사용되며 Unknown density 의 추정값 MISE는 위의 식과 같이 주어지게 된다.
위의 식에서 f는 Unknown density이고 , fn은 i.i.d에 기반한 n개의 Random Sample을 기반으로한 Estimation, E는 Expected value를 나타낸다.
다시 Bandwidth Selection으로 돌아와서 MISE(h)를 이용하여 Bandwidth optimal h를 구하게 된다.
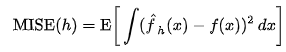
위의 식에서 f는 unknown real density function이다.
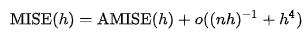
O는 O notation 이고 , n은 Sample의 사이즈 이다. AMISE는 aSymptotic MSIE로 AMISE의 식은 아래와 같이 표현된다.
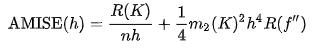
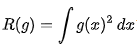
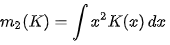
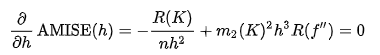
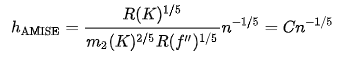
위 식에서 AMISE의 최소값은 위의 식의 해가 된다 .
그러나 위의 식은 Unknown density Function이 포함되어있어 직접적으로 사용할 수 없다.
여기서 h AMISE와 동일한 asymptotic order n^-1/5 가지는 Bandwidth를 AMISE에 대입하면 AMISE(h) = O(n^-4/5)가 된다.
만약 Bandwidth가 고정되어 있지 않고 Estmation 또는 Sample의 위치에 따라 달라지는 경우 Variable kernel density Estimation 방식은 커널의 크기가 샘플의 위치나 테스트 포인트의 위치에 따라 달라지는 커널 밀도 추정의 한 형태로 . 표본 공간이 다차원일 때 특히 효과적인 기술이다.
reference ; https://en.wikipedia.org/wiki/Kernel_density_estimation
Kernel Method란? (Kernel density estimation이란?) - Parzen window란? - 유니의 프로세스마이닝 공부 (tistory.com)
Kernel density estimation - Wikipedia
In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, base
en.wikipedia.org
'DataScience > Data' 카테고리의 다른 글
| [MLE]Maximum likelihood estimation에 대하여 (0) | 2022.01.26 |
|---|---|
| [Data processing] Smooth Bootstrap & Parametric Bootstrap (0) | 2022.01.25 |
| [Data processing]- Bayesian Bootstrap Method (0) | 2022.01.21 |
| [Data processing]Bootstrapping /Compiler/ Statistic/ ML 관점의 정리 (0) | 2022.01.21 |
| [interpolation] - Spline method (0) | 2022.01.08 |



