Bayesian Bootstrap
Bayesian Theorem
- Bayesian Statistic은 일반적인 Statistic 과 가장큰 차이가 Population을 미리 확정하지 않는 점이 가장 큰 차이점이다.
즉 Bayesian Theorem은 이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률을 추론하는 과정이다.
새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방식으로 베이지안 관점의 통계학에서는 사전 확률과 같은 경험에 기반한 선험적인, 혹은 불확실성을 내포하는 수치를 기반으로 하고, 거기에 추가 정보를 바탕으로 사전확률을 갱신하게 된다.

P(H) ; H의 사전 확률 ( prior probablistic , 과거의 경험적 확률 )
P(D|H) ; 사건 H가 주어졌을때, D의 조건부 확률 ( likelihood, 관찰된 결과에 기초한 어떤 가설에 대한 가능성 )
P(H|D) ; 사건 D라는 증거에 대한 사후 확률 ( posterior, 사건 D가 일어난 것을 알고, 그것이 사건 H로부터 일어난 것이라고 생각되는 조건부 확률 )
Bayesian Bootstrap(BB)
Bayesian Bootstrap은 일종의 Bayesian analogue Bootstrap이다. parameter(변수)를 추정하여 통계의 Sampling distribution을 시뮬레이션하는 대신 Bayesian Bootstrap은 PostError Distribution을 시뮬레이션하게 된다.
Bayesian Bootstrap replication은 observation data X set의 Sample CDF에서 0의 확률을 가지는것과같은 즉 관측되지 않은 Xset의 Posterior probability이 0인 각X의 Element로 Posterior probability을 생성하게 된다.
여기서 size n 과 Xset element x에 대한 Posterior Probability는 Size와 observation data Xset에 dependent하여 가변적이나 1/n을 중심으로 구성되게 된다.
특히 Bayesian Bootstrap replication은 n-1개의 0~1구간의 균일한 Random 변동성을 가진 u1,...,un-1을 기반으로 Gaps gn= un-un-1, u(0)=0 u(1)=1,인 g를 계산하게 된다.
여기서 g set = (g1, g2, ... ,gn )은 Bayesian Bootstrap Replication에서 Xset data X1, ..., Xn을 활용하여 접근한 확률 벡터이다.
예를들어보면 Φ는 observation data X set의 평균이라고하자 . Bayesian Bootstrap에서 observation data X의 평균을
∑ gx 로 계산을 할수 있게 된다. g는 X= x일때의 확률이다.
모든 Bayesian Bootstrap의 ∑ gx 의 값의 distribution은 X의 평균의 Bayesian Bootstrap distribution이 된다.
운영상 Bootstrap method와 Bayesian Bootstrap method는 x의 확률에 접근하는 방식은 매우 유사하다.
그리고 각각의 Replication에 대해 Expectation E( ) , Variance V( ) , Correlation C( ) 는
E( f ) = E( g ) = 1/n , V ( f ) = V( g ) (n+1)/n = (n-1)/n^3, C(f1,f2) = C(g1,g2) = -1/(n-1)이 된다.
결과적으로 Estimator Φ^의 형태는 Φ를 모방하도록 선택이 된다면 , 모든 f=g일때 Φ=Φ^의 Bayesian Bootstrap는 Φ의 bootstrap distribution 과 유사하게 된다.
그러나 결과적인 Distribution 해석의 영영에서 Baysian Bootstrap은 parameter Φ의 Posterior distribution을 시뮬레이션하지만 Bootstrap은 Φ를 추정하는 통계 Φ^의 sampling 분포를 시뮬레이션하므로 엄밀하게 다르다고 할 수 있다.
Bayesian BootStrap Theory
아래 식을 살펴보면 dk = (d1, .... ,dk)인 X의 모든 구별가능한 값의 벡터로 구성된다 . 그리고
Θ는 확률과 관련된 벡터이다.
X data set 은 i.i.d한 Sample이다. 여기서 Xset 데이터의 수를 nk라고한다면 dk와 nk는 같아지게 된다.
만약 Θ의 Prior distribution이 아래의 두번째 Θ식에 비례하게 된다면 Θ의 posterior distribution은 아래의 세번째 Θ에 비례하는 K-1 variate Dirichlet distribution이 된다.



이 posterior distribution은 independent하고 i,id 0~1구간에서 uniform한 random m-1개를 사용하여 시뮬레이션이진행되게 된다 . ( m= n + k + ∑l ) .
Uniform Uset 을 U(0,1)로 설정후 , Gap G set을 m개를 구성후 G set을 Kth Collection으로 분할을 진행한다.
Kth Collection은 n+l+1개의 element를 포함하고 Pset은 kth Collection의 g의 합으로 설정하게 된다.
이후 Pset은 k-1 variate D(n1+l1+1, ... , nk+lk+1 ) distribution을 따르게 되는데 . 결과적으로 각 obervation data x에 하나의 간격을 할당하게 되는 Bayesian Bootstrap 은 아래의 값에 비례하는 improper prior distribution에서 Θ의 posterior distribution를 시뮬레이션 하게 되고 Parameter Θ = Θ(Θ,d)의 posterior distribution을 시뮬레이션 하게 된다.

Θ^ set을 size n의 Sample에서 각 Dk와 동일한 값의 비율을 제공하는 통계라고 한다면 Θ^* set은 Θ^의 observed value인 nk/n이라고 할 수 있다.
Bayesian Bootstrap에서 Θ-Θ^*의 posterior distribution은 Θ = Θ^*라는 가정하에 Θ-Θ^의 distribution과 매우 유사하다고 할 수 있게 된다.
특히 두 Distribution의 평균은 0이고 , distribution의 kth element의 distribution은 아래와 같다

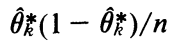
그리고 k및 k' 의 성분의 Distribution간 Correlation은 아래와 같이 나온다 .

REFERENCE
The Bayesian Bootstrap By Donald B. Rubin
'DataScience > Data' 카테고리의 다른 글
| [Data processing] Smooth Bootstrap & Parametric Bootstrap (0) | 2022.01.25 |
|---|---|
| KDE -Kernel Density Estimation 이란 ? (0) | 2022.01.25 |
| [Data processing]Bootstrapping /Compiler/ Statistic/ ML 관점의 정리 (0) | 2022.01.21 |
| [interpolation] - Spline method (0) | 2022.01.08 |
| [Data PreProcessing]TimeSeries-Smoothing 기법 정리 (1) | 2022.01.06 |



