[interpolation] - Spline method
이번 포스팅에서는 리뷰했던 논문 Density Forecasting for Long-Term Peak Electricity Demand 에서 나왔던 Spline에 대해 다루어 보고자한다.
Spline 이란 ?
스플라인 곡선(spline curve)은 주어진 복수의 제어점을 통과하는 부드러운 곡선으로, 인접한 두 점 사이에의 구간마다 별도의 다항식을 이용해 곡선을 정의한다고 정의한다.
n차 Spline Curve을 이용하면 n차 다항식을 의미하게되고 일반적으로 Spline curve는 3차 곡선을 이용한 보간법(interpolation) 으로 자주 이용되게된다.
여기서 polynomial interpolation은 한번에 모든 데이터를 사용하여 Curve를 생성하게 되지만 Spline interpolation은 data point를 쌍 사이의 곡선에 근사하고 모든 곡선을 더하여 최종적인 Estimated approximation을 구성하게 된다.
** A picewise continue function인 이유이다.
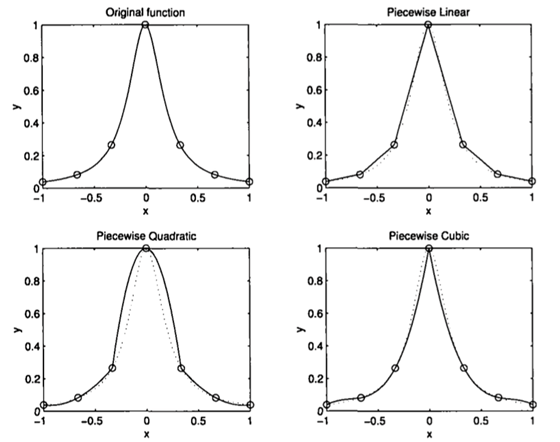
위 그리멩서 보면 picewise polynomial interpolation은 interval에 따라 polynomial을 적용하여 최대한 original function의 개형을 estimation하게 되는데 interval이 작을수록 accuracy가 증가하게 되는것을 볼수 있다.
즉 picewise interpolation은 각 junction에서 no continuously differentiable한 function의 개형을 얻게된다.
즉 함수를 추론했지만 사용하기에는 문제가 있다는 뜻이다 . 그렇기 떄문에 spline interpolation을 적용해야한다.
Basis function Y ( 기저함수 )
polynomial and piecewise-constant regression models과 regression splines가 모두 basis function에 속하게 된다.
basis function이란 변수 x에 적용 할수 있는 family of functions이나 transfomations( b1(x), b2(x),....bk(x) ) 를 사용하는 것이다.
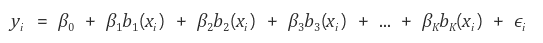
여기서 b1( . ) b2(.) ,..... bk(. )은 fixed 되어 있다면 무슨 값인지 알수 있는 값이다.
basis function의 특징은 Predictor b1(Xj), b2(Xj), .... , bk(Xj)에 대해 Standard Linear Model로 생각할 수 있기 때문에
계수를 추정하기 위한 least Squares나 선형 모델을 위한 모든 도구들을 사용할 수 있다는 것이다.
Spline Interpolation
inerpolation은 어떤 지점사이의 값을 기존의 값으로부터 추정하는 것을 의미한다.
즉 Spline Interpolation은 구간 사이에 별도의 다항식을 구하고 이를 통해 구간의 데이터를 추정하는것을 원칙으로 한다.
continuously하게 미분가능하면서 picewise polynomial approximation을 construct해야한다는 뜻이다.
여기서 spline은 각 Knot에서 자기 자신과 미분함수로 부터 (d-1)차수의 미분함수까지 모두 연속인 picewise degree-d 인 Polynomial이다.
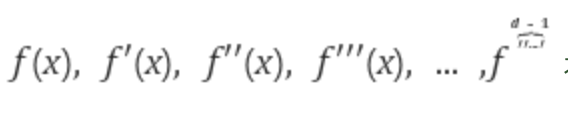
즉 위의 함수가 모두 연속인 함수 F(X)이다.
* knots는 함수의 계수가 변하는 구간으로 knots가 많을수록 더 flexible하게 된다.
linear Spline interpolation -1차 Spline Curve
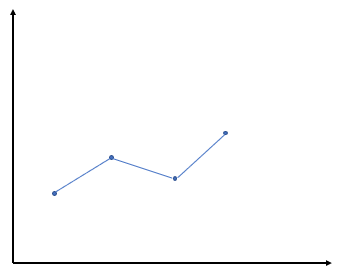
1차 Spline Curve는 linear Spline Interpolation으로 data point에 대해 인접한 두 포인트를 무조건 직선(1차식)으로 표현하여 추정하는 방식이다. 즉 두 point 사이의 기울기를 바탕으로 선형식을 구하는 방식이다.
Cubic Spline interpolation - 3차 Spline Curve
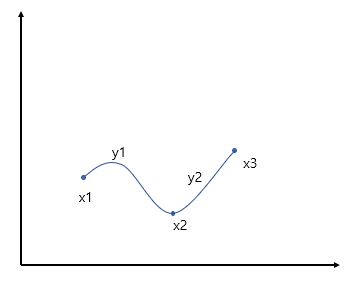
3차 Spline Curve는 Cubic Spline interpolation으로 3차 다항식을 사용하여 점사이의 데이터를 근사하게 된다.
인접한 두 data point의 양쪽에 Data를 하나씩 더추가하여 4개의 point를 3차 다항식으로 표현하여 더 smooth하게 만들어주는 방식이다.
위의 그림을 고려해보자면 x1, x2, x3가 존재할때 추론해야할 3차식은 y1, y2 두개가 존재한다
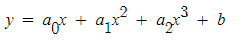
위의 일반항에서 a0 a1 a2 b 미지수를 구하기 위해서

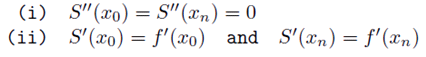
1. 각 식은 점을 지난다.
2. 각 식 y1, y2가 동시에 지나는 점에서의 값은 같다.
3. 동시에 지나는 점에서의 1차 미분값은 같다.
4. 동시에 지나는 점에서의 2차 미분값은 같다. 는 조건을 통하여 미지수를 구하게 된다. ( contineous 특성 )
5. 양 끝점에서2차 미분값이 0 이거나 특정값을 주어 제약을 걸수도 있다.
여기서 중요한 개념은 구간에서의 다항식을 추정하기 위해 제약식을 사용하게 되고 구간과 구간이 만나는 지점을 매끄럽게 연결하기 위함이다.
그러나 cubic spline은 monotonicity가 보장되지 않는다는 문제가 있다 . 원 데이터는 증가하지만 cubic spline으로 연결하게 된다면 내려가거나 상승하기만 하는 개형의 그래프를 얻게된다 .
그렇기때문에 제안되는 방식은 monotone Cubic Hermite interpolation method 이다.
※Fritsch, F. N.; Carlson, R.E. SIAM Journal on Numerical Analysis 1980 Monotone piecewise cubic interpolation, 17 (2) 238‐246, http://dx.doi.org/10.1137/0717021 참조
즉 전체 데이터를 하나의 다항식으로 구성하는게 아닌 전체 데이터가 구성하는 그래프를 보며 일정 구간을 a picewise continue 한 graph에서 부분 부분을 잘라내어( 잘라낸 지점의 위치는 NODE라고 한다 ) 구간별 다항식을 표현하는 방식이다.
이제 Spline이 Regression에서 어떤식으로 사용되는지 확인해 보고자한다 .
knots 구간이 변하는 지점 을 말한다.
1. Picewise polynomial regression
picewise polynomial regression은 전체 data에 대해 적합하는것이 아닌 범위를 지정(window size 혹은 bin size)하여 각 구간마다 regression을 적합하는 방식이다. 구간마다 regression을 진행한다는 것은 spline과 아주 유사하지만 picewise polynomial regression은 단순하게 다항식만 적합한다는 것이고 spline하지 않는다 ( spline은 derivative 성질역시 가지고 있다고 생각할 수 있다. )
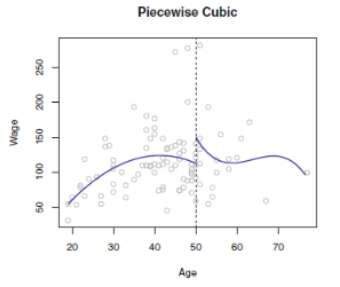
위의 그림을 보면 단순하게 각 구간이 x가 t인 지점에서 2개의 구간으로 나누어저 3차식을 적합하여 매끄럽게 continuously하지 않다.
즉 spline은 아니란 소리이며 또한 age가 50인 지점을 knots라고 말하게 된다.
2. Regression Splines
a picewise polynomial regression method에서 knots 지점의 discrite한 point를 이제 continuosly 하게 하기 위해 spline contidion이 활용되게 된다 . signal & system 과 고등수학에서 배웠던 미분가능 조건과 같이 2.) 두 식이 만나는 지점은 같은값이다 .6). 양끝점의 값을 특정 값으로 지정할 수 있다. 로 연속적인 형태의 함수를 구하게된다.
condition 1
2) 두 식이 만나는 지점은 동일한 값이다.
6) 양 끝점의 값은 특정 값으로 지정할 수 있다.
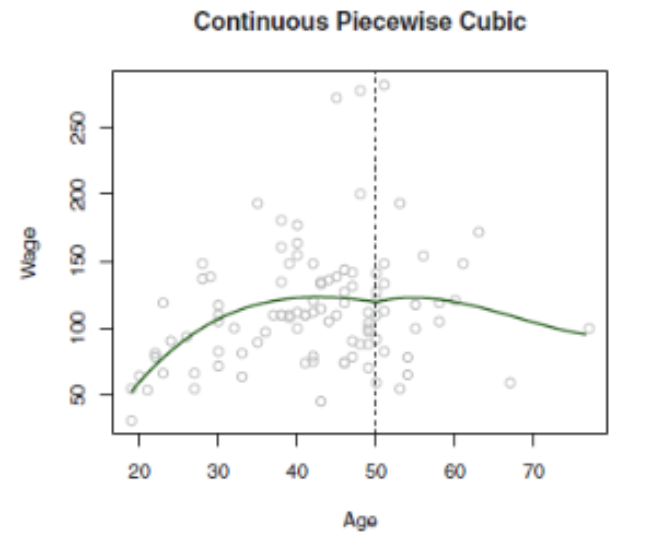
위의 조건을 구성하였지만 아직 전체적인 그래프 개형은 Age 50 인지점에서 미분계수가 다르기 때문에 함수 활용에 문제가 따른다 그렇기 떄문에 cubic spline 으로 적합하기 위해
condition2)
3 4 ) 미분값이 동일하다. ( 미분이 가능해야한다 )
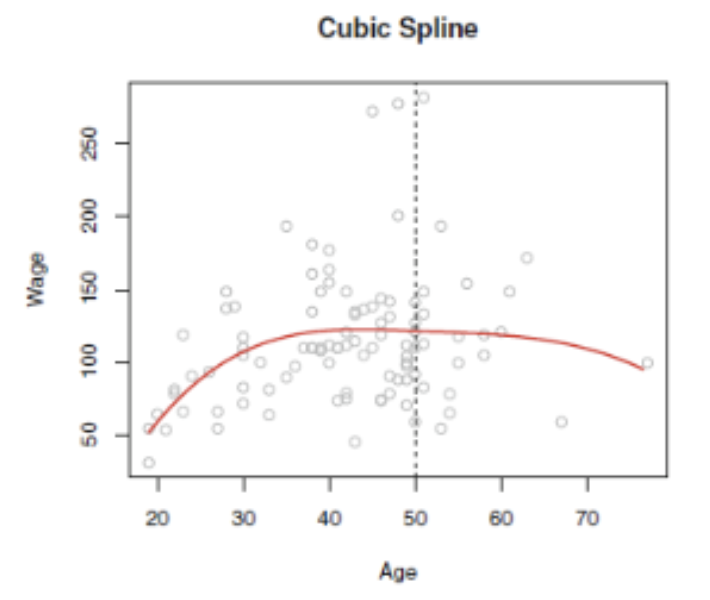
cubic spline 이 적합된 것을 확인할 수 있다. 위으 조건 2,3 ,4 ,6 )에 기반하여 식을 일반화하게 된다면
spline을 만족하기 위한 Degree dth차식은 각 knots에서 (d-1)차 까지 미분이 가능하고 연속이어야 한다.
해당 조건을 활용하기 위해 truncated power basis function을 활용하게 된다.
Truncatred Power Basis Function(TPB)
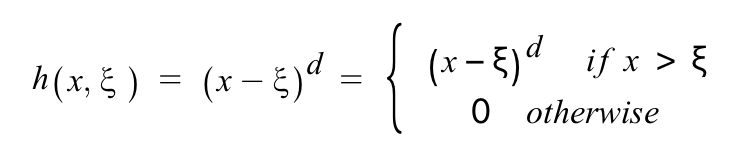
Truncatred Power Basis Function에서 function은 각 knots에서 d차식을 d-1차식까지 미분가능하고 연속이라는것을 표현한것이다.
℥은 knots를 의미한다.
d는 degree 를 의미한다.
k는 knots의 갯수를 의미한다.
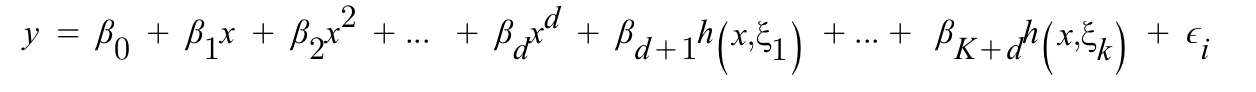
Truncatred Power Basis function을 활용하여 ploynomial baisis function을 일반화한 식이다.
위의 수식을 이해하기 위해 살펴보면 knot 가 1일 때, Truncatred Power Basis Function의 linear Spline은
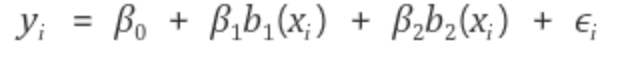
의 식으로 풀어지고 b1, b2는 아래와 같이 된다.
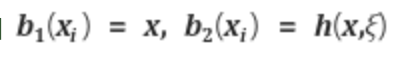
그러므로 위의 두 식을 풀게 되면 아래와 같이 정리할 수 있게 된다.
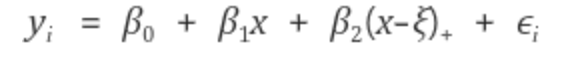
즉 위의 식을 참고하면 intercept와 d+k의 predictions를 least squares Regression을 이용해서 추정해주는 것이다.
Spline Regression을 진행하는 경우 spline의 구간 사이가 아닌 양 끝점에서 variance가 커지는 단점이 존재한다 .
즉 X가 매우 작거나 큰값을 가지는 경우에 variance가 커지는 현상에 해당하게 된다.
이러한 이슈를 해결하고자 Knot 의 양 끝 구간에 linear 적합을 사용하여 Natural Spline이라고 한다.
Natural Spline Regression + (additional boundary constraints )
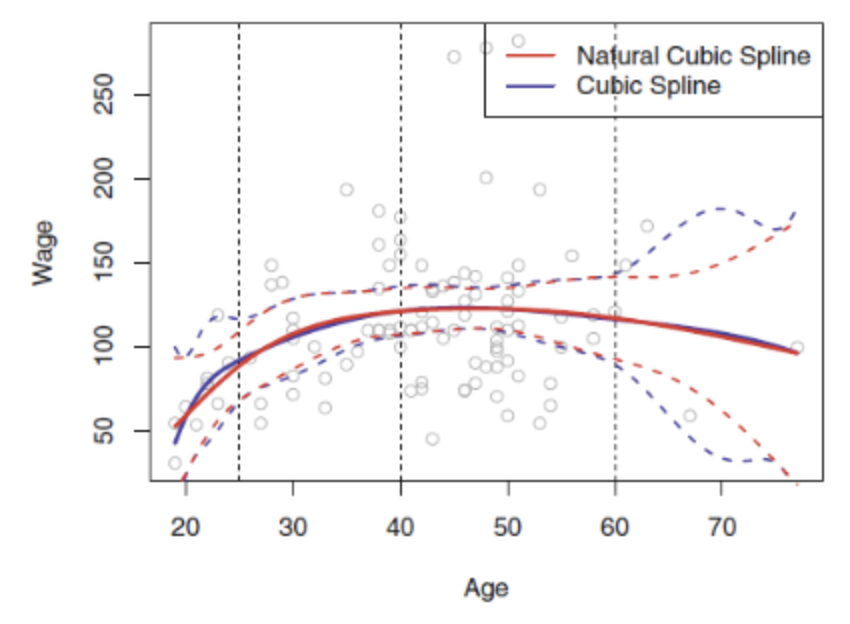
위 그림에서 점선은 신뢰구간 즉 Variance를 의미한다 . 즉 위의 그림을 보면 spline Regression 은 신뢰구간이 의 영역이 넓어지는 것을 볼수 있다 하지만 natural spline의 신뢰구간을 보게 되면 더 stable하다고 볼 수 있다.
Natural Spline은 additional Boundary Constraints를 추가한 것이다.
Additional Boundary Contraint는 가장 작은 knots보다 작거나 가장 큰 knot보다 큰 x에 해당하는 영역에서 함수가 Linear로 이어진다는 조건을 넣는 것이기 때문에 Linear 적합을 사용한다고 위에서 말하게 됐다.
Spline Regression에서 knot의 위치와 개수는 중요한 조건중에 하나이다.
일반적으로 Knots는 균등한 위치에 배치하여 백분위수를 활용하게 할 수 있다.
knot의 개수는 Cross-validation을 통해 knots의 개수에 따라 검증하여 적합한 knot의 개수를 선정할 수 있게 된다.
knots 위치 선정 조건
1. knots를 많이 포함하는 Regression splines은 개형을 더 flexible하게 만든다.
2. 이를 통해 함수가 급격하게 변하는 곳( 미분계수가 높은곳)은 knots를 많이 놓고 함수가 stable한 구간은 knots를 적게 놓는것이 효율적이다.
3. 이러한 방법이 잘 작용하기는 하지만 일반적으로 knot를 선정하는 방식은 아니다.
4. 구현 방법중에 하로 degrees of freedom을 specify한 다음 컴퓨팅연산을 통해 uniform quantile에 일정한 위치에 knots 를 선정하도록 한다.
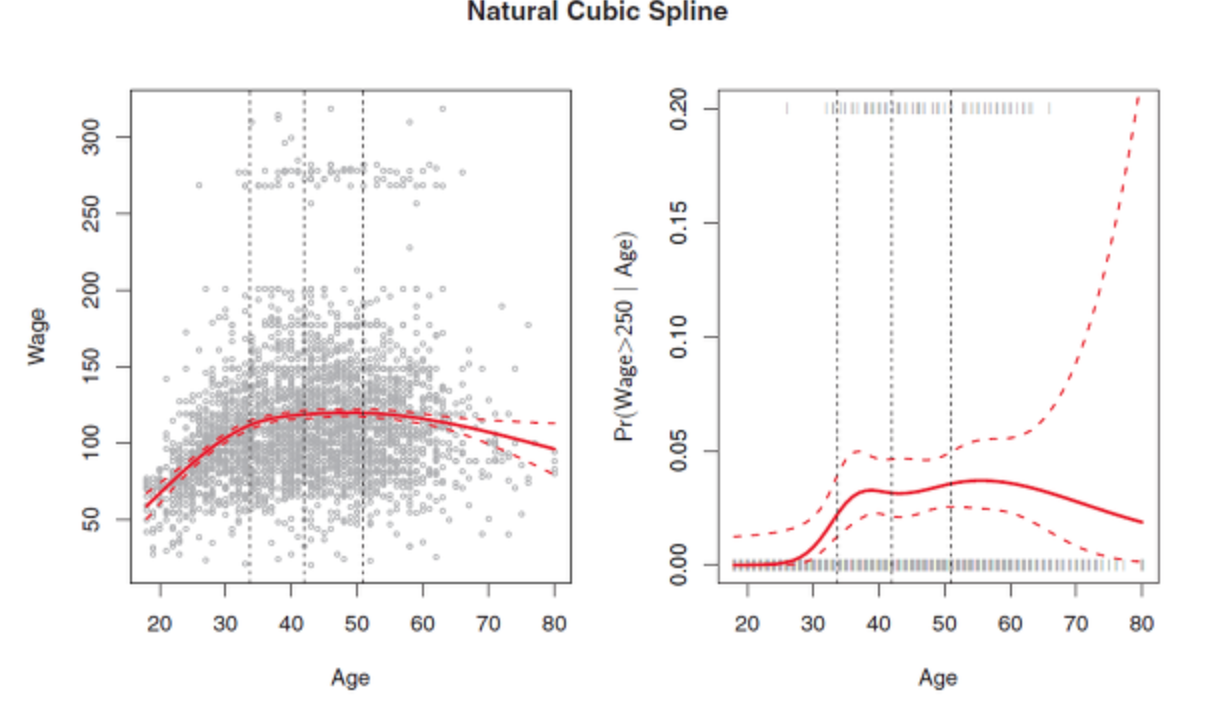
위 그림을 통해 확인할 수 있는것은 함수가 급격하게 변하는 구간에 Knots가 많이 놓여져 있으며 간격역시 일정하다는 조건을 확인할 수 있다.
knots 갯수 선정 조건
1. degrees of freedom을 몇으로 할지를 정하는 것과 동일하다.
2. 여러개의 knot를 시도한 후 (경험적으로) 다음에 가장 보기 좋은 (the best looking)곡선을 만드는 K를 고르게 된다.
2.1 cross validation을 이용하여 가장 작은 Cross-validation RSS를 만드는 k를 고르는 방법이있다.
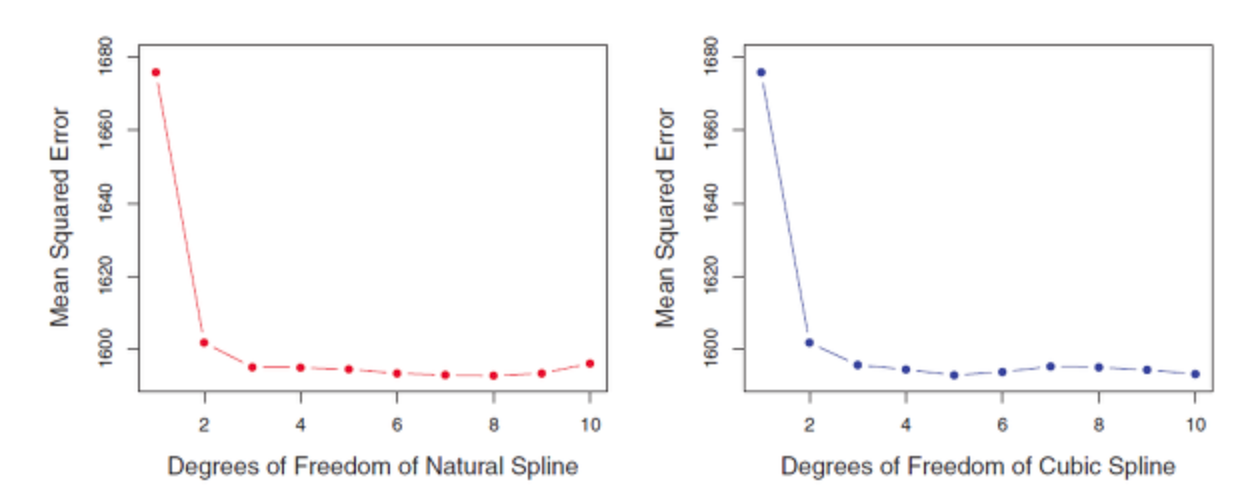
Spline Smoothing
Machine Learning 혹은 Deep learning에서 Training을 진행하게 될때 모델의 overfitting 문제에 직면하게 된다.
spline Regression 과 polynomial regression 역시 Overfitting problem에 대한 문제가 존재하며
데이터의 식에 따라 차수를 조절하며 접근하게 된다.
1. loss define
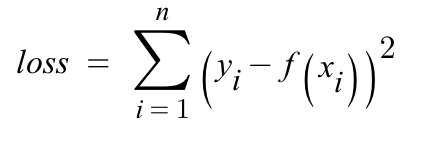
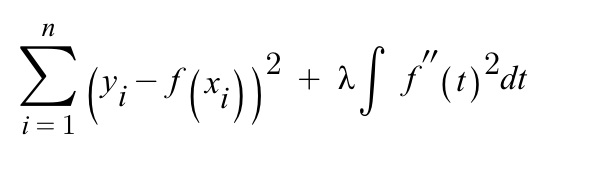
f(x)에 대한 값은 찾아야 하는 함수 개형이다. 오른쪽의 수식에서 λ∫ term 은 패널티 구간이며 λ는 0부터 무한대의 범위를 가지는 hyper parameter이다 . 패널티 구간에 대한 값은 2차 미분값으로 함수의 변동률에 대한 정보를 가지고 있게된다.
즉 함수가 unstable하게 변동한다는 뜻은 각 데이터와 관련하여 과적합가능성이 높은 high order equation F(x)로 도출이 된다는 의미라는 이야기가 된다.
loss 와 패널티 값을 토대로 데이터에서 추론한 개형 f(x)를 더 smooth한 형태로 만들게 되는것이 목적이 된다.
즉 smoothing 한 모델을 구하는 것이 목적이다.
spline regression에 대한 전반적인 것들을 수식과 함께 다루어 보았다. spline Regression의 장점은 X를 조각내어 즉 knot을 늘리게 되어 polynomial regression을 수행하게 된다. 이렇게 되면 기존의 복잡한 형태의 데이터를 분석하기 위해 고차원 다항식을 회귀식으로 쓰게 되며 overfittin과같은 문제에 직면하게 될수 있지만 spline regression을 사용여 knots의 수를 늘리게된다면 하나의 수식에 의존하지않고 각 knot구간마다 다항식을 정용하여 적합하기때문에 Overfitting의 가능성을 줄이게 된다.
하지만 hyper parameter로 쓰이는 knot의 수와 위치를 선정하는 것은 간단하지 않다는 단점이 있기도 하다.
결론적으로 Regression Spline이 polynomial regression보다 훨씬 좋은 결과를 낸다는점을 도출하게 된다.
import numpy as np
from scipy import interpolate
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
x = np.linspace(0 , 10 , num = 11, endpoint =True )
y = np.linspace(-x**2/9.0)
f = interp1d(x,y)
f2 = interp1d(x,y, kind='cubic')
xnew = np.linspace(0,10,num=41, endpoint=True)
plt.plot(x,y,'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data','linear','cubic'], loc= 'best')
plt.show()
#cubic spline
x = np.arange(0,2*np.pi/4, 2*np.pi/8)
y = np.sin(x)
tck = interpolate.splrep(x,y, s=0)
xnew = np.arrange(0,2*np.pi , np.pi/50)
ynew = interpolate.splev(xnew, tck, der= 0 )
plt.figure()
plt.plot(x,y,'x',xnew,ynew,xnew, np.sin(xnew), x,y, 'b')
plt.legend(['linear', 'cubic spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('cubic-spline interpolation')
plt.show()reference
James, Gareth, et al. An Introduction to Statical Learning. Springer. 2013